题目内容
已知函数
 (常数a>1>b>0).
(常数a>1>b>0).
(1)
求 的定义域;
的定义域;
(2)
在函数 的图象上是否存在不同的两点,使过此两点的直线平行于x轴;
的图象上是否存在不同的两点,使过此两点的直线平行于x轴;
(3)
当a、b满足什么关系时, 在
在 上恒取正值.
上恒取正值.
答案:略
解析:
提示:
解析:
|
(1) 由 得 得 ,由已知 ,由已知 ,故x>0,即函数 ,故x>0,即函数 的定义域为 的定义域为 . .
(2) 设 ,∵a>1>b>0, ,∵a>1>b>0,
∴  , , ,则 ,则 . .
故  , ,
∴ 
即  ,∴ ,∴ 在 在 上为增函数. 上为增函数.
假设函数  的图象上存在不同的两点 的图象上存在不同的两点 , , ,使直线AB平行于x轴,即 ,使直线AB平行于x轴,即 , , ,这与 ,这与 是增函数矛盾. 是增函数矛盾.
故函数  的图象上不存在不同的两点,使过这两点的直线平行于x轴. 的图象上不存在不同的两点,使过这两点的直线平行于x轴.
(3) 由(2)知 在 在 上是增函数. 上是增函数.
∴  在 在 上也是增函数. 上也是增函数.
∴当  时, 时, . .
∴只需  ,即 ,即 ,即 ,即 , , 时, 时, 在 在 上恒取正值. 上恒取正值. |
提示:
|
本题为对数指数问题的综合题,求定义域首先保证对数的真数为正,再利用指数运算性质求出定义域. (2)中证明是否存在要由单调性来确定,若单调递增或递减,就不存在两点连线平行于x轴. |

练习册系列答案
相关题目
 (常数a>1>b>0).
(常数a>1>b>0).
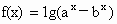 (常数a>1>b>0).
(常数a>1>b>0).