题目内容
若函数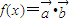 ,
,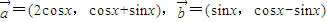 .
.(1)求f(x)的图象的对称中心坐标和对称轴方程;
(2)若
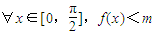 ,求实数m的取值范围.
,求实数m的取值范围.
【答案】分析:(1)先根据向量的数量积的坐标表示方法表示出函数f(x)的解析式,再由三角函数的两角和与差的正弦公式进行化简,最后根据三角函数的对称性可得答案.
(2)先根据x的范围求出2x+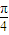 的范围,再由三角函数的图象可得答案.
的范围,再由三角函数的图象可得答案.
解答:解:∵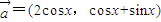 ,
,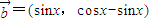 ,
,
∴f(x)=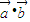 =2cosxsinx+(cosx+sinx)(cosx-sinx)
=2cosxsinx+(cosx+sinx)(cosx-sinx)
=sin2x+cos2x-sin2x=sin2x+cos2x
=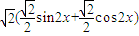 =
=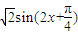
(1)令2x+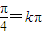 ,则x=
,则x=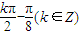
∴f(x)的图象的对称中心的坐标为(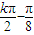 ,0)(k∈Z)
,0)(k∈Z)
令2x+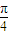 =k
=k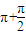 ,则得,x=
,则得,x=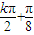 ,(k∈Z)
,(k∈Z)
∴f(x)的图象的对称轴方程为:x=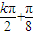 ,(k∈Z)
,(k∈Z)
(2)∵0≤x≤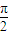 ∴
∴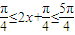
∴-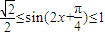
∴-1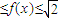 ∴m
∴m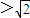
即m的取值范围是:(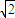 ,+∞)
,+∞)
点评:本题主要考查平面向量的数量积的坐标表示和三角函数的图象与性质的有关问题.属中档题.
(2)先根据x的范围求出2x+
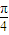 的范围,再由三角函数的图象可得答案.
的范围,再由三角函数的图象可得答案.解答:解:∵
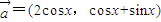 ,
,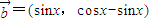 ,
,∴f(x)=
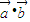 =2cosxsinx+(cosx+sinx)(cosx-sinx)
=2cosxsinx+(cosx+sinx)(cosx-sinx)=sin2x+cos2x-sin2x=sin2x+cos2x
=
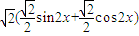 =
=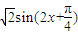
(1)令2x+
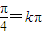 ,则x=
,则x=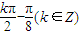
∴f(x)的图象的对称中心的坐标为(
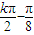 ,0)(k∈Z)
,0)(k∈Z)令2x+
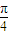 =k
=k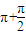 ,则得,x=
,则得,x=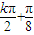 ,(k∈Z)
,(k∈Z)∴f(x)的图象的对称轴方程为:x=
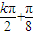 ,(k∈Z)
,(k∈Z)(2)∵0≤x≤
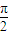 ∴
∴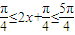
∴-
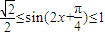
∴-1
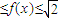 ∴m
∴m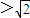
即m的取值范围是:(
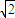 ,+∞)
,+∞)点评:本题主要考查平面向量的数量积的坐标表示和三角函数的图象与性质的有关问题.属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
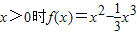
 上的值域为
上的值域为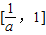 ,求a的值.
,求a的值.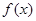 是定义在(0,+∞)上的增函数,并满足
是定义在(0,+∞)上的增函数,并满足
 ,求m的值
,求m的值 <2求x的范围
<2求x的范围 ,若函数
,若函数 且
且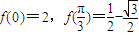 .
.