题目内容
设点A(x1,f(x1)),B(x2,f(x2)),T(x0,f(x0))在函数f(x)=x3-ax(a>0)的图象上,其中x1,x2是f(x)的两个极值点,x0(x0≠0)是f(x)的一个零点,若函数f(x)的图象在T处的切线与直线AB垂直,则a=________.

分析:先把函数的零点求出来,再对函数f(x)求导并求出其零点,列出表格和画出图象,利用在斜率存在的条件下两条直线垂直的充要条件k1k2=-1即可求出答案.
解答:令f(x)=0,(a>0),则
 ,解得x=0,
,解得x=0, .
.
∵x0(x0≠0)是f(x)的一个零点,∴
 或
或 .
.∵f′(x)=3x2-a=
 ,
,令f′(x)=0,解得
 ,列表如下:
,列表如下:由表格可知:当x=
 时,函数f(x)取得极小值,且
时,函数f(x)取得极小值,且 ;
;当x=-
 时,函数f(x)取得极大值,且
时,函数f(x)取得极大值,且 =
= ;
;不妨设A
 ,B
,B .∴
.∴ .
. 根据表格作出如下图象:
根据表格作出如下图象:①当
 时.
时. =2a,
=2a,∵函数f(x)的图象在T处的切线与直线AB垂直,
∴
 ,(a>0),解得
,(a>0),解得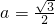 .
.②当
 时.
时. =2a,
=2a,∵函数f(x)的图象在T处的切线与直线AB垂直,
∴
 ,(a>0),解得a=
,(a>0),解得a= .
.综上可知:满足条件的a的值为
 .
.故答案为
 .
.点评:充分利用导数研究函数的性质和理解函数的零点是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目