题目内容
4．求到点A（-5，0）和B（5，0）的距离的平方差为36的动点的轨迹方程．分析 设动点P（x，y），利用已知条件列出方程，求出点的轨迹方程．
解答 解：设动点P（x，y），P到点A（-5，0）和B（5，0）的距离的平方差为36，
则PA2=（x+5）2+（y-0）2，
PB2=（x-5）2+（y-0）2，
所以|PA2-PB2|=36，
|20x|=36，
得：x=$±\frac{9}{5}$
所求解方程为：x=$±\frac{9}{5}$．
点评 本题考查点的轨迹方程的求法，是中档题，解题时要认真审题，注意两点间距离公式的合理运用．
练习册系列答案
相关题目
15．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}-1（x≤0）}\\{f（x-1）（x＞0）}\end{array}\right.$，若函数y=f（x）-x-$\frac{a}{2}$恰有两个不同的零点，则实数a的取值范围是（ ）
| A． | （0，2） | B． | （-∞，2） | C． | （-∞，2] | D． | [0，+∞） |
12．已知f（x）、g（x）、h（x）均为一次函数．若对实数x满足：
|f（x）|-|g（x）|+h（x）=$\left\{\begin{array}{l}{-2，x＜-1}\\{7x+5，-1≤x＜0}\\{-4x+5，x≥0}\end{array}\right.$，h（x）的解析式为．
|f（x）|-|g（x）|+h（x）=$\left\{\begin{array}{l}{-2，x＜-1}\\{7x+5，-1≤x＜0}\\{-4x+5，x≥0}\end{array}\right.$，h（x）的解析式为．
| A． | 2x-$\frac{3}{2}$ | B． | -2x-$\frac{3}{2}$ | C． | 2x+$\frac{3}{2}$ | D． | -2x+$\frac{3}{2}$ |
16．
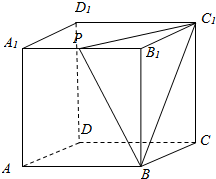如图，在棱长为2的正方体ABCD-A1B1C1D1中，A1B1的中点是P，过点A1作截面PBC1平行的截面，则该截面的面积为（ ）
如图，在棱长为2的正方体ABCD-A1B1C1D1中，A1B1的中点是P，过点A1作截面PBC1平行的截面，则该截面的面积为（ ）| A． | 2$\sqrt{2}$ | B． | 2$\sqrt{3}$ | C． | 2$\sqrt{6}$ | D． | 4 |