Question

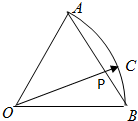如图，在半径为1的扇形AOB中，∠AOB=60°，C为弧上的动点，AB与OC交于点P，则

OP

•

BP

的最小值是

 

．

Answer 1

分析：根据题意，可以得到△OAB为等边三角形，则AB=1，设BP=x，则AP=1-x，（0≤x≤1），利用向量加法的三角形法则，将则

OP

•

BP

向已知向量转化，运用向量数量积的定义，即可得到关于x的二次函数，利用二次函数的性质，即可求得答案．

解答：解：∵OA=OB=1，∠AOB=60°，
∴△OAB为等边三角形，则AB=1，
设BP=x，则AP=1-x，（0≤x≤1），
∴

OP

•

BP

=（

OA

+

AP

）•

BP

=

OA

•

BP

+

AP

•

BP

=|

OA

|•|

BP

|cos＜

OA

，

BP

＞+|

AP

|•|

BP

|cos＜

AP

，

BP

＞
=1•x•cos

π

3

+（1-x）•x•cosπ
=x2-

1

2

x
=（x-

1

4

）²-

1

16

，
∵0≤x≤1，
∴当x=

1

4

时，

OP

•

BP

取得最小值为-

1

16

．
故答案为：-

1

16

．

点评：本题考查了平面向量数量积的运算，解决平面向量数量积的问题，一般有三种方法：向量转化法，坐标化法，特殊值法．解题的关键是运用向量加法和减法的三角形法则或平行四边形法则，将要求的向量一步一步向已知的向量转化．属于中档题．