题目内容
已知点A(-1,0),B(1,-1)和抛物线C:y2=4x,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图
(1)证明: 为定值;
为定值;
(2)若△POM的面积为 ,求向量
,求向量 与
与 的夹角;
的夹角;
(3)证明直线PQ恒过一个定点.
(1)证明:
 为定值;
为定值;(2)若△POM的面积为
 ,求向量
,求向量 与
与 的夹角;
的夹角;(3)证明直线PQ恒过一个定点.

解:(1)设点
∵P、M、A三点共线,
∴ kAM=kPM,
即
即 ,
,
∴y1y2=4,


即 为定值.
为定值.
(2)解:设∠POM=α,则 ·cosα=5.
·cosα=5.
∵ ,
, ·sinα=5.
·sinα=5.
由此可得tanα=1,又α∈(0,π),
∴α=45°,
故向量 与
与 的夹角为45°.
的夹角为45°.
(3)证明:设点 ,
,
∵M、B、Q三点共线,
∴kBQ= kOM ,
即 ,
,
即
∴(y3+1)(y1+y3)=
即y1y3+y1+y3+4=0.
由(1)知y1y2=4,即
∴
即4(y2+y3)+y2y3+4=0.(*)
∵
∴直线PQ的方程是
(y-y2)(y2+y3)=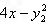
即y(y2+y3)-y2y3=4x
由(*)式,得-y2y3=4(y2+y3)+4,代入上式,得(y+4)(y2+y3)=4(x-1).
由此可知直线PQ过定点(1,-4)。

∵P、M、A三点共线,
∴ kAM=kPM,
即

即
 ,
,∴y1y2=4,


即
 为定值.
为定值.(2)解:设∠POM=α,则
 ·cosα=5.
·cosα=5.∵
 ,
, ·sinα=5.
·sinα=5.由此可得tanα=1,又α∈(0,π),
∴α=45°,
故向量
 与
与 的夹角为45°.
的夹角为45°.(3)证明:设点
 ,
,∵M、B、Q三点共线,
∴kBQ= kOM ,
即
 ,
,即

∴(y3+1)(y1+y3)=

即y1y3+y1+y3+4=0.
由(1)知y1y2=4,即

∴

即4(y2+y3)+y2y3+4=0.(*)
∵

∴直线PQ的方程是

(y-y2)(y2+y3)=
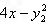
即y(y2+y3)-y2y3=4x
由(*)式,得-y2y3=4(y2+y3)+4,代入上式,得(y+4)(y2+y3)=4(x-1).
由此可知直线PQ过定点(1,-4)。

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.
如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.