题目内容
设f(x)=4cos(ωx﹣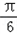 )sinωx-cos(2ωx+π),其中ω>0。
)sinωx-cos(2ωx+π),其中ω>0。
(1)求函数y=f(x)的值域
(2)若f(x)在区间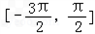 上为增函数,求ω的最大值。
上为增函数,求ω的最大值。
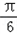 )sinωx-cos(2ωx+π),其中ω>0。
)sinωx-cos(2ωx+π),其中ω>0。(1)求函数y=f(x)的值域
(2)若f(x)在区间
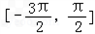 上为增函数,求ω的最大值。
上为增函数,求ω的最大值。解:(1)f(x)=4cos(ωx﹣ )sinωx-cos(2ωx+π)=4(
)sinωx-cos(2ωx+π)=4( cosωx+
cosωx+ sinωx)sinωx+cos2ωx
sinωx)sinωx+cos2ωx
=2 cosωxsinωx+
cosωxsinωx+ sin2ωx+cos2ωxsin2ωx=
sin2ωx+cos2ωxsin2ωx= sin2ωx+1,
sin2ωx+1,
∵-1≤sin2ωx≤1,所以函数y=f(x)的值域是[ ]。
]。
(2)因y=sinx在每个区间[ ],k∈z上为增函数,
],k∈z上为增函数,
令 ,
,
又ω>0,
所以,解不等式得 ≤x≤
≤x≤ ,
,
即f(x)= sin2ωx+1,(ω>0)在第个闭区间[
sin2ωx+1,(ω>0)在第个闭区间[ ,
, ],k∈z上是增函数又有题设f(x)在区间
],k∈z上是增函数又有题设f(x)在区间 上为增函数
上为增函数
所以 ?[
?[ ,
, ],对某个k∈z成立,
],对某个k∈z成立,
于是有
解得ω≤ ,故ω的最大值是
,故ω的最大值是 。
。
 )sinωx-cos(2ωx+π)=4(
)sinωx-cos(2ωx+π)=4( cosωx+
cosωx+ sinωx)sinωx+cos2ωx
sinωx)sinωx+cos2ωx=2
 cosωxsinωx+
cosωxsinωx+ sin2ωx+cos2ωxsin2ωx=
sin2ωx+cos2ωxsin2ωx= sin2ωx+1,
sin2ωx+1,∵-1≤sin2ωx≤1,所以函数y=f(x)的值域是[
 ]。
]。(2)因y=sinx在每个区间[
 ],k∈z上为增函数,
],k∈z上为增函数,令
 ,
,又ω>0,
所以,解不等式得
 ≤x≤
≤x≤ ,
,即f(x)=
 sin2ωx+1,(ω>0)在第个闭区间[
sin2ωx+1,(ω>0)在第个闭区间[ ,
, ],k∈z上是增函数又有题设f(x)在区间
],k∈z上是增函数又有题设f(x)在区间 上为增函数
上为增函数所以
 ?[
?[ ,
, ],对某个k∈z成立,
],对某个k∈z成立,于是有

解得ω≤
 ,故ω的最大值是
,故ω的最大值是 。
。
练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 )sinωx-cos(2ωx+π),其中ω>0.
)sinωx-cos(2ωx+π),其中ω>0. 上为增函数,求ω的最大值.
上为增函数,求ω的最大值.