题目内容
如图所示,在棱长为2的正方体ABCD﹣A1B1C1D1中,E、F分别为DD1、DB的中点.
(1)求证:EF⊥B1C;
(2)求三棱锥B1﹣EFC的体积.
(1)求证:EF⊥B1C;
(2)求三棱锥B1﹣EFC的体积.
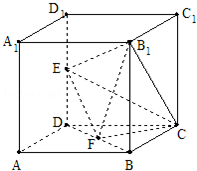
(1)证明:连接BD1,BC1
∵E、F分别为DD1、BD的中点
∴EF∥BD1
∵正方体ABCD﹣A1B1C1D1
∴D1C1⊥平面BCC1B1
∴D1C1⊥B1C
∵正方形BCC1B1
∴B1C⊥BC1
∵D1C1∩BC1=C1
∴B1C⊥平面BC1D1
∴B1C⊥BD1
∵EF∥BD1
∴EF⊥B1C
(2)解:∵CB=CD,BF=DF
∴CF⊥BD
∵DD1⊥平面ABCD
∴DD1⊥CF
又DD1∩BD=D
∴CF⊥平面BDD1B1
又CF=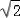
∵EF⊥平面B1FC
∴EF⊥FB1EF=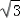 ,FB1=
,FB1=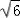
Rt△B1EF的面积=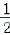 ×EF×FB1=
×EF×FB1= ×
×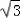 ×
×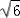 =
=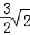
∴V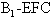 =V
=V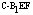 =
= ×S△
×S△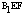 ×CF=
×CF=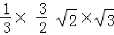 =1
=1
∴三棱锥B1﹣EFC的体积为1.
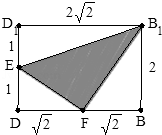
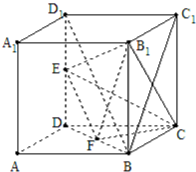
∵E、F分别为DD1、BD的中点
∴EF∥BD1
∵正方体ABCD﹣A1B1C1D1
∴D1C1⊥平面BCC1B1
∴D1C1⊥B1C
∵正方形BCC1B1
∴B1C⊥BC1
∵D1C1∩BC1=C1
∴B1C⊥平面BC1D1
∴B1C⊥BD1
∵EF∥BD1
∴EF⊥B1C
(2)解:∵CB=CD,BF=DF
∴CF⊥BD
∵DD1⊥平面ABCD
∴DD1⊥CF
又DD1∩BD=D
∴CF⊥平面BDD1B1
又CF=
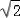
∵EF⊥平面B1FC
∴EF⊥FB1EF=
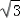 ,FB1=
,FB1=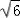
Rt△B1EF的面积=
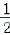 ×EF×FB1=
×EF×FB1= ×
×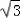 ×
×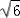 =
=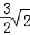
∴V
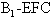 =V
=V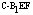 =
= ×S△
×S△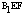 ×CF=
×CF=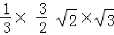 =1
=1∴三棱锥B1﹣EFC的体积为1.



练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
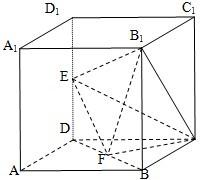 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.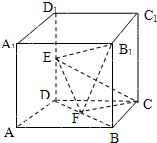 17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点
17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点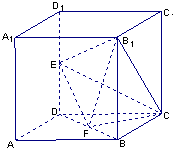 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点. 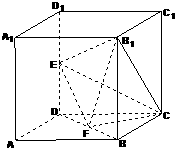 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.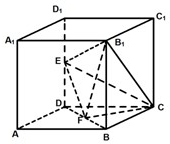 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.