题目内容
【题目】已知二次函数![]() 满足
满足![]() ,
,![]() .
.
![]() 求函数
求函数![]() 的解析式;
的解析式;
![]() 若关于x的不等式
若关于x的不等式![]() 在
在![]() 上恒成立,求实数t的取值范围;
上恒成立,求实数t的取值范围;
![]() 若函数
若函数![]() 在区间
在区间![]() 内至少有一个零点,求实数m的取值范围
内至少有一个零点,求实数m的取值范围
【答案】(1)f(x)=2x2-6x+2; (2)t>10; (3)m<-10或m≥-2.
【解析】
(1)用待定系数法设二次函数表达式,再代入已知函数方程化简即可得答案; (2)分离参数后求f(x)的最大值即可;(3)先求无零点时m的范围,再求补集.
(1)设二次函数f(x)=ax2+bx+2,(a≠0)
∴a(x+1)2+b(x+1)+2-ax2-bx-2=4x-4
∴2ax+a+b=4x-4,
∴a=2,b=-6
∴f(x)=2x2-6x+2;
(2)依题意t>f(x)=2x2-6x+2在x∈[-1,2]上恒成立,
而2x2-6x+2的对称轴为x=![]() ∈[-1,2],
∈[-1,2],
所以x=-1时,取最大值10,
t>10;
(3)∵g(x)=f(x)-mx=2x2-6x+2-mx=2x2-(6+m)x+2在区间(-1,2)内至少有一个零点,当g(x)在(-1,2)内无零点时,△=(6+m)2-16<0或 或,
或,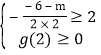 解得:-10≤m<-2,
解得:-10≤m<-2,
因此g(x)在(-1,2)内至少有一个零点时,m<-10或m≥-2.

练习册系列答案
相关题目