题目内容
已知：如图，一个圆的两条弦AB和CE相交于点D，BE=2，BC=2BD=2
，∠1=∠2则EC=________，∠CBE=________．
4 90°
分析：利用弧所对的圆周角相等，可知∠1=∠EBD，从而△EBD∽△ECB，故可得比例线段，进而可解．．
解答：∵∠1=∠2，∴∠1=∠EBD
∴△EBD∽△ECB
∴
∴
，∴EC=4
根据EB2+BC2=EC2，可知∠CBE=90°
故答案为4，90°
点评：本题的考点是与圆有关的比例线段，主要考查同弧所对的圆周角相等，关键是构造相似形，从而得比例线段．
分析：利用弧所对的圆周角相等，可知∠1=∠EBD，从而△EBD∽△ECB，故可得比例线段，进而可解．．
解答：∵∠1=∠2，∴∠1=∠EBD
∴△EBD∽△ECB
∴
∴
，∴EC=4根据EB2+BC2=EC2，可知∠CBE=90°
故答案为4，90°
点评：本题的考点是与圆有关的比例线段，主要考查同弧所对的圆周角相等，关键是构造相似形，从而得比例线段．
练习册系列答案
全优点练单元计划系列答案
相关题目
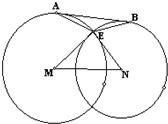已知：如图，E是相交两圆⊙M和⊙N的一个交点，且ME⊥NE，AB为外公切线，切点分别为A，B连接AE，BE，则∠AEB的度数为
已知：如图，一个圆的两条弦AB和CE相交于点D，BE=2，BC=2BD=2
，∠1=∠2则EC= ，∠CBE= ．
