题目内容
若P(x,y)在圆(x-2)2+y2=3上运动,则| y | x-4 |
分析:本题考查的知识点是简单线性规划的应用,我们先画出满足约束条件(x-2)2+y2=3的几何图形,然后分析
的几何意义,分析圆上的点的情况,即可得到
的取值范围.
| y |
| x-4 |
| y |
| x-4 |
解答: 解:画出满足约束条件(x-2)2+y2=3的几何图形如下图示:
解:画出满足约束条件(x-2)2+y2=3的几何图形如下图示:
∵
表示(4,0)点于点P连线斜率,
又由于圆的半径为
,
易得过(4,0)点作圆的切线斜率分别为:±
故
的最小值等于-
故答案为:-
 解:画出满足约束条件(x-2)2+y2=3的几何图形如下图示:
解:画出满足约束条件(x-2)2+y2=3的几何图形如下图示:∵
| y |
| x-4 |
又由于圆的半径为
| 3 |
易得过(4,0)点作圆的切线斜率分别为:±
| 3 |
故
| y |
| x-4 |
| 3 |
故答案为:-
| 3 |
点评:平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 的参数方程为
的参数方程为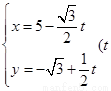 为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 .
.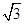 x +y的取值范围.
x +y的取值范围. +y2=1上运动时f(P)=5是否能成立?若能求出P点坐标,若不能,说明理由.
+y2=1上运动时f(P)=5是否能成立?若能求出P点坐标,若不能,说明理由.