题目内容

△ABC的三个内角A、B、C满足下列条件：(1)A＜B＜C;(2)A、B、C成等差数列；(3)tanA·tanC=2+.

(1)求A、B、C的大小；

(2)若AB上的高为4，求a、b、c的大小.

解：(1)由题意知B=60°，A+C=120°,tan(A+C)==-tanB=-,

    ∴tanA+tanC=3+.

    故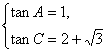

    或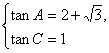(舍).

    故A=45°,B=60°,C=75°.

    (2)过C作CD⊥AB于D，则CD=4.

    在Rt△ACD和Rt△ABC中，由正弦定理得

    a==8,b==4,c=AD+DB=4+4.

练习册系列答案
相关题目
已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若a=1，b=
3
，A+C=2B，则sinC=（　　）
A、0B、2C、1D、-1
△ABC的三个内角A、B、C的对边分别是a，b，c，给出下列命题：
①若sinBcosC＞-cosBsinC，则△ABC一定是钝角三角形；
②若sin2A+sin2B=sin2C，则△ABC一定是直角三角形；
③若bcosA=acosB，则△ABC为等腰三角形；
④在△ABC中，若A＞B，则sinA＞sinB；
其中正确命题的序号是
②③④
②③④
．（注：把你认为正确的命题的序号都填上）
已知△ABC的三个内角A，B，C的对边分别为a，b，c，且a，b，c成等比数列
（1）若sinC=2sinA，求cosB的值；
（2）求角B的最大值．并判断此时△ABC的形状．
已知a，b，c分别为△ABC的三个内角A，B，C的对边，
m
=(-
3
，sinA)，
n
=(cosA，1)，且
m
⊥
n
．
（Ⅰ）求角A的大小；
（Ⅱ）若a=2，△ABC的面积为
3
，求b，c．
已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若a=1，b=
3
，B=60°，则sinC=
1
1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网