题目内容
在等比数列{an}中,首项为a1,公比为q,Sn表示其前n项和.
(I)记Sn=A,S2n-Sn=B,S3n-S2n=C,证明A,B,C成等比数列;
(II)若 ,
, ,记数列{log2an}的前n项和为Tn,当n取何值时,Tn有最小值.
,记数列{log2an}的前n项和为Tn,当n取何值时,Tn有最小值.
解:( I)当q=1时,A=na1,B=2na1-na1=na1,
C=3na1-2na1=na1,可见A,B,C成等比数列;
当q≠1时,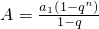 ,
,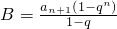 ,
,
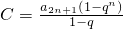 .故有
.故有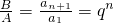
,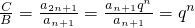 .
.
可得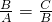 ,这说明A,B,C成等比数列.
,这说明A,B,C成等比数列.
综上,A,B,C成等比数列;
(II)若q=1,则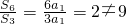 ,
,
与题设矛盾,此情况不存在;
若q≠1,则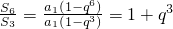 ,
,
故有1+q3=9,解得q=2. (8分)
所以an=a•2n-1,可知log2an=n-1+log2a.
所以数列{log2an}是以log2a为首项,1为公差的等差数列.
令log2an≤0,即n-1+log2a≤0?n≤1-log2a.
因为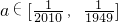 ,
,
所以log2a∈[-log22010,-log21949],
即得1-log2a∈[1+log21949,1+log22010],
可知满足log2an≤0的最大的n值为11.
所以,数列{log2an}的前11项均为负值,
从第12项开始都是正数.因此,当n=11时,Tn有最小值.
分析:( I)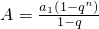 ,
,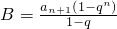 ,
,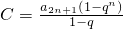 .故
.故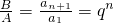 ,
,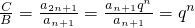 .所以A,B,C成等比数列;
.所以A,B,C成等比数列;
(II)若q=1,则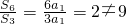 ,与题设矛盾;若q≠1,则
,与题设矛盾;若q≠1,则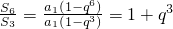 ,故有1+q3=9,解得q=2.
,故有1+q3=9,解得q=2.
所以an=a•2n-1,可知log2an=n-1+log2a.由此入手能够推导出当n=11时,Tn有最小值.
点评:本题考查数列的性质和应用,解题时要注意公式的合理运用.
C=3na1-2na1=na1,可见A,B,C成等比数列;
当q≠1时,
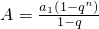 ,
,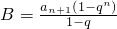 ,
,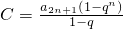 .故有
.故有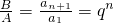
,
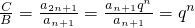 .
.可得
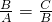 ,这说明A,B,C成等比数列.
,这说明A,B,C成等比数列.综上,A,B,C成等比数列;
(II)若q=1,则
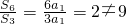 ,
,与题设矛盾,此情况不存在;
若q≠1,则
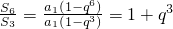 ,
,故有1+q3=9,解得q=2. (8分)
所以an=a•2n-1,可知log2an=n-1+log2a.
所以数列{log2an}是以log2a为首项,1为公差的等差数列.
令log2an≤0,即n-1+log2a≤0?n≤1-log2a.
因为
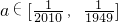 ,
,所以log2a∈[-log22010,-log21949],
即得1-log2a∈[1+log21949,1+log22010],
可知满足log2an≤0的最大的n值为11.
所以,数列{log2an}的前11项均为负值,
从第12项开始都是正数.因此,当n=11时,Tn有最小值.
分析:( I)
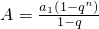 ,
,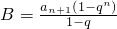 ,
,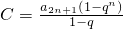 .故
.故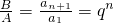 ,
,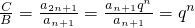 .所以A,B,C成等比数列;
.所以A,B,C成等比数列;(II)若q=1,则
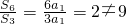 ,与题设矛盾;若q≠1,则
,与题设矛盾;若q≠1,则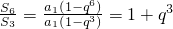 ,故有1+q3=9,解得q=2.
,故有1+q3=9,解得q=2.所以an=a•2n-1,可知log2an=n-1+log2a.由此入手能够推导出当n=11时,Tn有最小值.
点评:本题考查数列的性质和应用,解题时要注意公式的合理运用.

练习册系列答案
相关题目
在等比数列{an}中,若a1=1,公比q=2,则a12+a22+…+an2=( )
| A、(2n-1)2 | ||
B、
| ||
| C、4n-1 | ||
D、
|