Question

在直角坐标系xOy中，点B与点A（-1，0）关于原点O对称．点P（x₀，y₀）在抛物线y²=4x上，且直线AP与BP的斜率之积等于2，则x₀=________．

Answer 1

分析：利用关于原点的对称性即可得出点B的坐标，利用斜率的计算公式即可得出x₀与y₀的关系式，把点P代入抛物线C的方程又得到一个关系式，联立即可得出x₀．
解答：∵点B与点A（-1，0）关于原点O对称，∴B（1，0）．
∴，，
∵k_AP•k_BP=2，
∴，
又∵点P（x₀，y₀）在抛物线y²=4x上，∴．
代入得到，化为，
解得=．
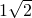∵x₀＞0，
∴x₀=．
故答案为．
点评：熟练掌握中心对称性、斜率的计算公式、点在曲线上即满足曲线的方程解出即可．