题目内容
设f (x)是奇函数,且在(0,+∞)上是增函数,又f (-3)=0,则x·f (x)<0的解集为
| A.{x∣-3<x<0或x>3} |
| B.{x∣x<-3或0<x<3} |
| C.{x∣x<-3或x>3} |
| D.{x∣-3<x<0或0<x<3} |
D.
解析试题分析:有题意易知,f(3)=0,f(x)在(-∞,0)上是增函数;由数形结合可知:当x<-3或0<x<3时,f(x)<0;当-3<x<0或x>3时,f(x)>0.所以x·f (x)<0的解集为{x∣-3<x<0或0<x<3}。
考点:本题考查函数单调性和奇偶性的灵活应用。
点评:本题的关键是根据单调性和奇偶性利用数形结合思想分析出f(x)的正负。

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
若 ,则
,则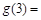 ( )
( )
A. | B. | C. | D. |
设 ,则
,则 的解集为
的解集为
A. | B. | C. | D. |
若关于x的方程 (a>0,且
(a>0,且 )有解,则m的取值范围是( )
)有解,则m的取值范围是( )
A. | B. | C. | D. |
方程 的根的个数是( )
的根的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
函数 ,
,  ,则函数值
,则函数值 的取值范围是( )
的取值范围是( )
A.{ ≤ ≤ ≤5} ≤5} | B. | C.{ } } | D. |
已知函数 的值域是
的值域是 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
若幂函数 的图像不过原点,且关于原点对称,
的图像不过原点,且关于原点对称,
则 的取值是
的取值是
A. | B. |
C. | D. |
下列函数中,在区间 上是增函数的是 ( )
上是增函数的是 ( )
A. | B. | C. | D. |