题目内容
已知数列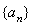 的前n项和为
的前n项和为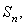
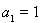 ,
,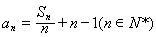
(1)求证:数列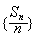 为等差数列;
为等差数列;
(2)设数列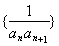 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn.
【答案】
(1)由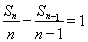 ,即得数列
,即得数列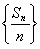 为等差数列;(2)
为等差数列;(2)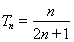 .
.
【解析】
试题分析:(1)由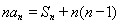 ,
,
得到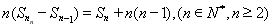
即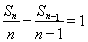 ,作出结论.
,作出结论.
(2)由(1)得: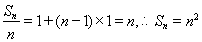 ,
,
得到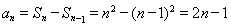 ,
,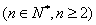 ,
,
从而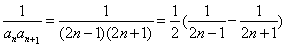
利用“裂项相消法”求和.
试题解析:(1)由题意可得: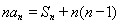 ,
,
∴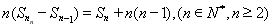 3分
3分
即: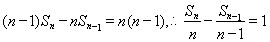 ,
,
所以数列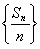 为等差数列; 6分
为等差数列; 6分
(2)由(1)得: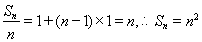 ,
,
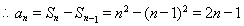 ,
,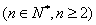 9分
9分
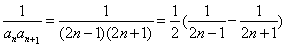
 , 12分
, 12分
考点:等差数列的概念,“裂项相消法”.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 求使不等式
求使不等式 的前n项和为
的前n项和为 ,
, 且满足
且满足 +n (n>1且n∈
+n (n>1且n∈ )
) ,求使得不等式
,求使得不等式 成立的最小正整数n的值
成立的最小正整数n的值  的前n项和为
的前n项和为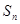 ,且
,且 ,
, ,并猜想
,并猜想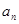 的表达式。
的表达式。