题目内容
已知数列![]() 的前N项和为
的前N项和为![]()
(1)证明:数列![]() 是等比数列;
是等比数列;
(2)对 求使不等式
求使不等式![]() 恒成立的自然数
恒成立的自然数![]() 的最小值.
的最小值.
(1)见解析(2)5
解析:
(1)![]()
![]()
又当![]() 时,
时,![]() ,
,
![]()
![]() ------------------------------------------------------4分
------------------------------------------------------4分
![]() ∴数列
∴数列![]() 是公比为2,首项为
是公比为2,首项为![]() 的等比数列.……2分
的等比数列.……2分
(2)由(1),知![]()
![]()
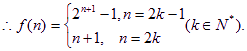 …………………………………………4分
…………………………………………4分
①当m为偶数时,![]() ,
,
∴不存在自然数m,使![]() 恒成立. …………………………2分
恒成立. …………………………2分
②当m为奇数时,![]()
当m=1时,![]() ;
;
当m=3时,![]() ;-----------------------2分
;-----------------------2分
当m=5时,![]() ;
;
当m≥5时,即证:![]() 恒成立
恒成立
ⅰ)![]() ,已证
,已证
ⅱ)假设![]()
![]() ,结论成立,即
,结论成立,即![]()
则![]() 时,
时,![]()
而![]()
则![]()
即 ![]() 时,结论成立
时,结论成立
所以当m≥5且为奇数,![]() 成立, -------------3分
成立, -------------3分
此时m的最小值为5. ----------------------------------------------------1分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前n项和为
的前n项和为 ,
, 且满足
且满足 +n (n>1且n∈
+n (n>1且n∈ )
) ,求使得不等式
,求使得不等式 成立的最小正整数n的值
成立的最小正整数n的值  的前n项和为
的前n项和为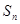 ,且
,且 ,
, ,并猜想
,并猜想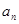 的表达式。
的表达式。