题目内容

设f（x）=sin2x+mcos2x，若对一切x∈R，都有f（x）≤f(
π
8
)，则f(
π
24
)=
6
2
6
2
．
分析：设出sinφ和cosφ，利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数，根据题意得到x=
π
8
时，函数取得最值，故把x=
π
8
代入函数解析式，求出的函数值等于最值±
m2+1
，列出关于m的方程，求出方程的解得到m的值，从而确定出函数解析式，把x=
π
24
的值代入即可求出f（
π
24
）的值．
解答：解：由题意知：
f（x）=sin2x+mcos2x=
m2+1
sin（2x+φ），（sinφ=
m
m2+1
，cosφ=
1
m2+1
）
由题意得：当x=
π
8
时函数f（x）=sin2x+mcos2x取到最值±
m2+1
，
将x=
π
8
代入可得：sin（2×
π
8
）+mcos（2×
π
8
）=
2
2
(m+1)=±
m2+1
，即m=1
∴f（x）=sin2x+mcos2x=sin2x+cos2x=
2
sin（2x+
π
4
），
则f（
π
24
）=
2
sin（2×
π
24
+
π
4
）=
2
sin
π
3
=
6
2
．
故答案为：
6
2
点评：此题考查了两角和与差的正弦函数，正弦函数的单调性，以及特殊角的三角函数值，灵活运用两角和与差的正弦函数公式及特殊角的三角函数值把函数解析式化为一个角的正弦函数是本题的突破点．
练习册系列答案
相关题目
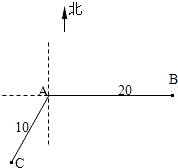精英家教网如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西30°，相距10海里C处的乙船．
（Ⅰ）求处于C处的乙船和遇险渔船间的距离；
（Ⅱ）设乙船沿直线CB方向前往B处救援，其方向与
CA
成θ角，求f（x）=sin2θsinx+cos2θcosx（x∈R）的值域．
设φ∈(0，
π
4
)，函数f（x）=sin2（x+φ），且f(
π
4
)=
3
4
．
（Ⅰ）求φ的值；
（Ⅱ）若x∈[0，
π
2
]，求f（x）的最大值及相应的x值．
（2012•湖北）设函数f（x）=sin2ωx+2
3
sinωx•cosωx-cos2ωx+λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（
1
2
，1）．
（1）求函数f（x）的最小正周期；
（2）若y=f（x）的图象经过点(
π
4
，0)，求函数f（x）的值域．
（2012•许昌一模）设函数f（x）=sin2（x+
π
4
）-cos2（x+
π
4
）（x∈R），则函数f（x）是（　　）
设|φ|＜
π
4
，函数f（x）=sin2（x+φ）．若f（
π
4
）=
3
4
，则φ等于（　　）
A、-
π
12
B、-
π
6
C、
π
12
D、
π
6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网