题目内容
已知椭圆的两个焦点分别为F1(0,-8),F2(0,8),且椭圆上一点到两个焦点的距离之和为20,则此椭圆的方程为 .
分析:利用已知条件,结果椭圆的定义,先求出焦点位置和a,c的值,由此能求出椭圆方程.
解答:解:∵椭圆的两个焦点分别为F1(0,-8),F2(0,8),
∴该椭圆的焦点坐标在y轴上,且c=8,
∵椭圆上一点到两个焦点的距离之和为20,
∴2a=20,即a=10,
∴b2=102-82=36,
∴此椭圆的方程为
+
=1.
故答案为:
+
=1.
∴该椭圆的焦点坐标在y轴上,且c=8,
∵椭圆上一点到两个焦点的距离之和为20,
∴2a=20,即a=10,
∴b2=102-82=36,
∴此椭圆的方程为
| x2 |
| 100 |
| y2 |
| 36 |
故答案为:
| x2 |
| 100 |
| y2 |
| 36 |
点评:本题考查椭圆的标准方程的求法,解题时要熟练掌握椭圆的定义和性质,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
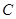 :
:
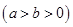 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足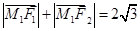 .
.
 作直线
作直线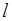 ,使得直线
,使得直线 .求出
.求出 的值.
的值. :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足 .
. (0,
(0,  )
) ,使得过点
,使得过点 与椭圆
与椭圆 .若存在,请求出
.若存在,请求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。 :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足 .
.
 作直线
作直线 ,使得直线
,使得直线 .求出
.求出 的值.
的值.