题目内容
给定椭圆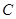 :
:
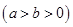 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆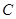 的“伴随圆”. 已知椭圆
的“伴随圆”. 已知椭圆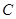 的两个焦点分别是
的两个焦点分别是 ,椭圆
,椭圆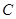 上一动点
上一动点 满足
满足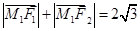 .
.
(Ⅰ)求椭圆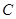 及其“伴随圆”的方程;
及其“伴随圆”的方程;
(Ⅱ)过点P
 作直线
作直线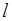 ,使得直线
,使得直线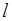 与椭圆
与椭圆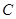 只有一个交点,且
只有一个交点,且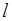 截椭圆
截椭圆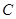 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为 .求出
.求出 的值.
的值.
【答案】
(Ⅰ) (Ⅱ)
(Ⅱ)
【解析】 (1)中据椭圆定义及伴椭圆定义容易求出方程;
(2)线 与椭圆
与椭圆 只有一个交点即直线与椭圆相切,
只有一个交点即直线与椭圆相切, ,
,
 截椭圆
截椭圆 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为 ,利用直线与圆弦心距,点到直线距离公式,表示出弦长
,利用直线与圆弦心距,点到直线距离公式,表示出弦长
解:(Ⅰ)由题意得: 得
得 ,半焦距
,半焦距 ....2分
....2分
则 椭圆
椭圆 的方程为
的方程为 “伴随圆”的方程为
“伴随圆”的方程为
(Ⅱ)设过点 ,且与椭圆有一个交点的直线
,且与椭圆有一个交点的直线 为
为 ,
,
则  整理得
整理得 .........2分
.........2分
所以
 ,解
,解 ①........4分
①........4分
又因为直线 截椭圆
截椭圆 的“伴随圆”所得的弦长为
的“伴随圆”所得的弦长为 ,
,
则有 化简得
化简得 ② ....6分
② ....6分
联立① ②解得,
②解得, ,所以
,所以

练习册系列答案
相关题目
 :
:
 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为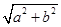 的圆是椭圆
的圆是椭圆 ,且其短轴上的一个端点到
,且其短轴上的一个端点到 的距离为
的距离为 .
. 是椭圆
是椭圆 ,使得
,使得 :
: ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为 .
. 是椭圆
是椭圆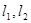 使得
使得 ,求证:
,求证: 为定值.
为定值. :
: ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是
的圆是 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距
的距 .
. 是椭圆
是椭圆 使得
使得 ;
; 轴正半轴的交点时,求
轴正半轴的交点时,求 为定值.
为定值. :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足 .
.
 作直线
作直线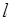 ,使得直线
,使得直线 .求出
.求出 的值.
的值.