题目内容
17.设函数f(x)=mx2-2x+m,若函数f(x)有且只有一个正实数的零点,求实数m的取值范围.分析 由题意,讨论函数f(x)=mx2-2x+3是一次函数还是二次函数,从而求解.
解答 解:(1)当m=0时,f(x)=-2x与x轴交于原点,不满足要求.
(2)当m≠0时,要使得f(x)=mx2-2x+m只有一个正实数零点,
则$\left\{\begin{array}{l}△=4-4{m}^{2}=0\\ \frac{1}{m}>0\end{array}\right.$,
解得:m=1,
综上所述,m=1
点评 本题考查了函数的零点与方程的根的关系,属于基础题.

练习册系列答案
相关题目
7.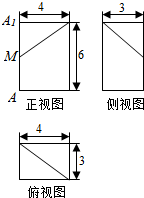 若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )
若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )
 若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )
若某几何体的三视图如图所示,其中A1M:AM=7:5.则此几何体的体积等于( )| A. | 55 | B. | 62 | C. | 65 | D. | 72 |
 已知四棱锥S-ABCD中,SD⊥平面ABCD,E是SC中点,O是底面正方形ABCD的中心,AB=SD,OF⊥SB,垂足为F
已知四棱锥S-ABCD中,SD⊥平面ABCD,E是SC中点,O是底面正方形ABCD的中心,AB=SD,OF⊥SB,垂足为F