题目内容
(2012•道里区三模)在△ABC中,角A、B、C所对的边分别为a、b、c,且acosB-bcosA=
c,当tan(A-B)取最大值时,角C的值为
.
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
分析:利用正弦定理及诱导公式化简已知的等式,整理后利用同角三角函数间的基本关系弦化切后得到tanA=3tanB,利用两角和与差的正切函数公式化简tan(A-B),将tanA=3tanB代入,利用基本不等式变形,求出tan(A-B)取得最大值时tanA与tanB的值,进而确定出A与B的度数,即可此时得到C的度数.
解答:解:利用正弦定理化简已知的等式得:sinAcosB-sinBcosA=
sinC=
sin(A+B)=
(sinAcosB+cosAsinB),
整理得:sinAcosB=3cosAsinB,
两边除以cosAcosB得:tanA=3tanB,
则tan(A-B)=
=
=
,
∵A、B是三角形内角,且tanA与tanB同号,
∴A、B都是锐角,即tanA>0,tanB>0,
∴3tanB+
≥2
,当且仅当3tanB=
,即tanB=
时取等号,
∴tanA=3tanB=
,
∴A=
,B=
,
则C=
.
故答案为:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得:sinAcosB=3cosAsinB,
两边除以cosAcosB得:tanA=3tanB,
则tan(A-B)=
| tanA-tanB |
| 1+tanAtanB |
| 2tanB |
| 1+3tan2B |
| 2 | ||
3tanB+
|
∵A、B是三角形内角,且tanA与tanB同号,
∴A、B都是锐角,即tanA>0,tanB>0,
∴3tanB+
| 1 |
| tanB |
| 3 |
| 1 |
| tanB |
| ||
| 3 |
∴tanA=3tanB=
| 3 |
∴A=
| π |
| 3 |
| π |
| 6 |
则C=
| π |
| 2 |
故答案为:
| π |
| 2 |
点评:此题考查了两角和与差的正切函数公式,正弦定理,同角三角函数间的基本关系,诱导公式,以及基本不等式的运用,熟练掌握公式及定理是解本题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
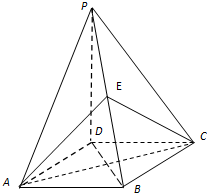 (2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. (2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=
(2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=