题目内容
设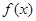 与
与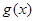 是定义在同一区间
是定义在同一区间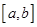 上的两个函数,若对任意的
上的两个函数,若对任意的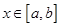 ,都有
,都有 ,则称
,则称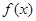 和
和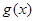 在
在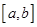 上 是“密切函数”,
上 是“密切函数”,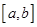 称为“密切区间”,设
称为“密切区间”,设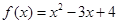 与
与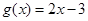 在
在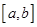 上是“密切函数”,则它的“密切区间”可以是 ( )
上是“密切函数”,则它的“密切区间”可以是 ( )
A.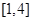 | B.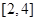 | C.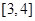 | D. |
D
解析试题分析:由题意由 ,得
,得 ,解之得
,解之得 ,故选D.
,故选D.
考点:1.含绝对值的一元二次不等式的解法;2.函数新定义题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知一元二次不等式 的解集为
的解集为 ,则
,则 的解集为 ( )
的解集为 ( )
A. | B.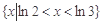 |
C. | D.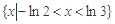 |
关于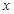 的不等式
的不等式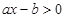 的解集是
的解集是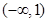 ,则关于
,则关于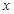 的不等式
的不等式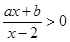 的解为( )
的解为( )
A. | B.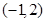 | C.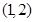 | D.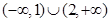 |
若不等式 对于一切非零实数
对于一切非零实数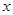 均成立,则实数
均成立,则实数 的取值范围是( )
的取值范围是( )
A.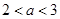 | B.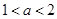 | C.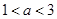 | D.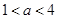 |
不等式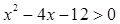 的解集是
的解集是
A.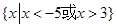 | B.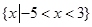 |
C.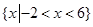 | D.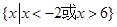 |
若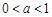 ,则不等式
,则不等式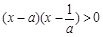 的解集为 ( )
的解集为 ( )
A. | B.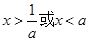 | C.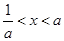 | D.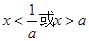 |
a∈R,且a2+a<0,那么-a,-a3,a2的大小关系是( )
| A.a2>-a3>-a | B.-a>a2>-a3 |
| C.-a3>a2>-a | D.a2>-a>-a3 |
已知函数 ,
,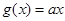 ,对于任意
,对于任意 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. | B.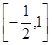 | C. | D. |
设函数f(x)= ,已知f(a)>1,则a的取值范围是( )
,已知f(a)>1,则a的取值范围是( )
A.(-∞,-2)∪( ,+∞) ,+∞) |
B.( , , ) ) |
C.(-∞,-2)∪( ,1) ,1) |
D.(-2, )∪(1,+∞) )∪(1,+∞) |