题目内容
直线y=x+b与曲线2y=
有两个不同的公共点,则实数b∈( )
| 20-x2 |
分析:曲线表示以F1(-
,0),F2(
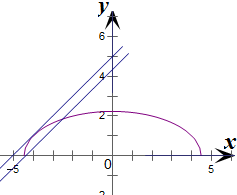
,0)为焦点的上半个椭圆,当直线y=x+b与上半个椭圆有两个不同的相点时,满足条件.
| 15 |
| 15 |
解答:解:∵2y=
∴
+
=1(y≥0)即表示以F1(-
,0),F2(
,0)为焦点的上半个椭圆,
结合图象可知直线应介于图中两平行线的位置满足条件
当直线过左顶点(-2
,0)时b=2
当直线与椭圆相切时,设切点为(m,
)
切线的斜率为1=f′(m)=
解得m=-4
∴切点为(-4,1),而切点在直线y=x+b上,则b=5
∴直线y=x+b与曲线2y=
有两个不同的公共点,则实数b∈[2
,5)
故选D.
| 20-x2 |

∴
| x2 |
| 20 |
| y2 |
| 5 |
| 15 |
| 15 |
结合图象可知直线应介于图中两平行线的位置满足条件
当直线过左顶点(-2
| 5 |
| 5 |
当直线与椭圆相切时,设切点为(m,
| 1 |
| 2 |
| 20-m2 |
切线的斜率为1=f′(m)=
| -m | ||
2
|
∴切点为(-4,1),而切点在直线y=x+b上,则b=5
∴直线y=x+b与曲线2y=
| 20-x2 |
| 5 |
故选D.
点评:本题考查了直线和椭圆的位置关系,主要考查了直线与椭圆相交的性质以及导数的几何意义,体现了数形结合及函数与方程的数学思想,属于中档题.

练习册系列答案
相关题目
若直线y=x-b与曲线
(θ∈[0,2π))有两个不同的公共点,则实数b的取值范围为( ).
|
A、(2-
| ||||
B、[2-
| ||||
C、(-∞,2-
| ||||
D、(2-
|
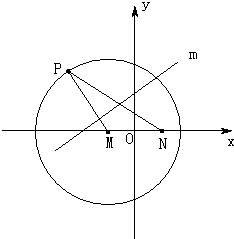 如图,已知
如图,已知