题目内容
 (2013•青岛二模)某几何体的三视图如图所示,当这个几何体的体积最大时,以下结果正确的是( )
(2013•青岛二模)某几何体的三视图如图所示,当这个几何体的体积最大时,以下结果正确的是( )分析:三视图复原几何体是长方体的一个角,设出棱长,利用勾股定理,基本不等式,求出最大值.
解答: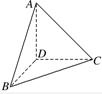 解答:解:如图所示,可知AC=
解答:解:如图所示,可知AC=
,BD=1,BC=b,AB=a.
设CD=x,AD=y,
则x2+y2=6,x2+1=b2,y2+1=a2,
消去x2,y2得.
a2+b2=8≥
,
所以a+b≤4,
当且仅当a=b=2时等号成立,此时x=
,y=
,几何体的体积最大.
故选D.
 解答:解:如图所示,可知AC=
解答:解:如图所示,可知AC=| 6 |
设CD=x,AD=y,
则x2+y2=6,x2+1=b2,y2+1=a2,
消去x2,y2得.
a2+b2=8≥
| (a+b)2 |
| 2 |
所以a+b≤4,
当且仅当a=b=2时等号成立,此时x=
| 3 |
| 3 |
故选D.
点评:本题考查三视图求体积,考查基本不等式求最值,是中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2013•青岛二模)一同学为研究函数f(x)=
(2013•青岛二模)一同学为研究函数f(x)=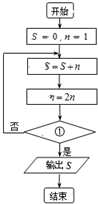 (2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )
(2013•青岛二模)执行如图所示的程序框图.若输出S=31,则框图中①处可以填入( )