题目内容
已知抛物线过点（1，1），则该抛物线的标准方程是 ．
分析：设出抛物线的方程，根据点与抛物线的关系代入即可求解．
解答：解：若抛物线的交点在x轴，设抛物线的方程为y2=mx，m≠0，
∵抛物线过点（1，1），
∴1=m，即m=1，
∴此时抛物线方程为y2=x．
若抛物线的交点在y轴，设抛物线的方程为x2=ny，n≠0，
∵抛物线过点（1，1），
∴1=n，即n=1，
此时抛物线方程为x2=y．
综上：y2=x或x2=y，
故答案为：y2=x或x2=y
∵抛物线过点（1，1），
∴1=m，即m=1，
∴此时抛物线方程为y2=x．
若抛物线的交点在y轴，设抛物线的方程为x2=ny，n≠0，
∵抛物线过点（1，1），
∴1=n，即n=1，
此时抛物线方程为x2=y．
综上：y2=x或x2=y，
故答案为：y2=x或x2=y
点评：本题主要考查抛物线方程的求法，利用待定系数法是解决本题的关键，比较基础．
练习册系列答案
相关题目
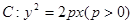过点
。
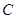的标准方程，并求其准线方程；
(
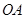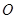为坐标原点）的直线
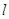，使得直线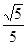
?
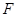作两条斜率存在且互相垂直的直线
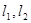，设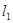
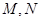与抛物线
，
与抛物线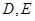
，求
的最小值。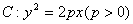
过点A（1，-2）。
，使得直线
？若存在，求出直线