题目内容
(本题满分13分)已知抛物线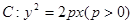 过点
过点 。
。
(1)求抛物线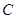 的标准方程,并求其准线方程;
的标准方程,并求其准线方程;
(2)是否存在平行于 (
( 为坐标原点)的直线
为坐标原点)的直线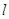 ,使得直线
,使得直线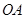 与
与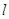 的距离等于
的距离等于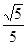 ?
?
若存在,求直线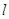 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
(3)过抛物线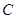 的焦点
的焦点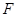 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线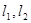 ,设
,设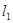 与抛物线
与抛物线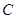 相交于点
相交于点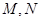 ,
, 与抛物线
与抛物线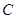 相交于点
相交于点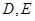 ,求
,求 的最小值。
的最小值。
【答案】
(1) 抛物线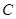 的方程为
的方程为 ,其准线方程为
,其准线方程为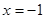 (2)
符合题意的直线
(2)
符合题意的直线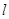 存在,其方程为
存在,其方程为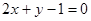 (3)
(3)
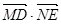 的最小值为16.
的最小值为16.
【解析】
试题分析:(1)将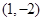 带入
带入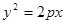 ,得
,得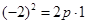 ,所以
,所以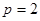 ,
,
故所求抛物线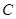 的方程为
的方程为 ,其准线方程为
,其准线方程为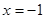 . ……2分
. ……2分
(2)假设存在符合题意的直线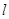 ,其方程为
,其方程为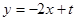 ,
,
由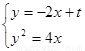 得
得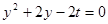 , ……3分
, ……3分
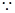 直线
直线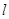 与抛物线
与抛物线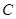 有公共点,
有公共点,
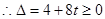 解得
解得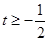 , ……4分
, ……4分
由直线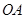 与
与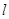 的距离
的距离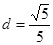 可得
可得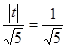 ,解得
,解得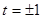 , ……5分
, ……5分
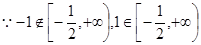 ,
,
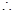 符合题意的直线
符合题意的直线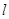 存在,其方程为
存在,其方程为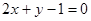 . ……7分
. ……7分
(3)由题意知,直线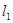 的斜率存在且不为0,设为
的斜率存在且不为0,设为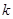 ,则
,则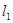 的方程为
的方程为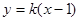 ,
,
由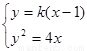 ,得
,得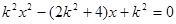 ,
,
设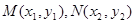 ,则
,则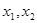 是上述方程的两个实根,
是上述方程的两个实根,
于是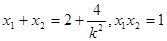 ,
,
因为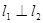 ,所以斜率为
,所以斜率为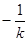 ,
,
设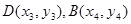 ,则同理可得
,则同理可得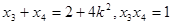 。
。
故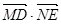 =
=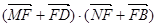 =
=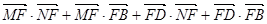
=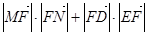 =
=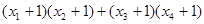
=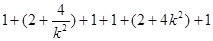
= ,
,
当且仅当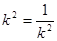 ,即
,即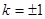 时
时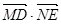 取最小值
取最小值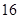 . ……13分
. ……13分
考点:本小题主要考查双曲线标准方程的求法和直线与双曲线的位置关系的应用以及平面向量的坐标运算、基本不等式的应用等,考查学生综合运用所学知识解决问题的能力和运算求解能力.
点评:直线与圆锥曲线的位置关系问题是高考考查的重点内容,且一般出在压轴题的位置,难度较大,主要是运算量较大,所以要充分利用数形结合思想的应用,尽量简化运算.

练习册系列答案
相关题目
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
. 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.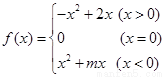 为奇函数;
为奇函数;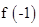 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
 取得最小值时点P的坐标.
取得最小值时点P的坐标.  是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆 于
于 两点
两点 ,求直线
,求直线 的方程;
的方程; 恒过一定点.
恒过一定点.