题目内容
在单调递增数列{an}中,a1=1,a2=2,且a2n-1,a2n,a2n+1成等差数列,a2n,a2n+1,a2n+2成等比数列,n=l,2,3,….
(Ⅰ)分别计算a3,a5和a4,a6的值;
(Ⅱ)求数列{an}的通项公式(将an用n表示);
(Ⅲ)设数列 的前n项和为Sn,证明:
的前n项和为Sn,证明: ,n∈N*。
,n∈N*。
(Ⅰ)分别计算a3,a5和a4,a6的值;
(Ⅱ)求数列{an}的通项公式(将an用n表示);
(Ⅲ)设数列
 的前n项和为Sn,证明:
的前n项和为Sn,证明: ,n∈N*。
,n∈N*。 解:(Ⅰ)由已知得 。
。
(Ⅱ) ,
, ,…
,…
 ,…
,…
∴猜想: ,
,
以下用数学归纳法证明之。
①当n=1时, ,猜想成立;
,猜想成立;
②当n=k(k≥1,k∈N*)时,猜想成立,即 ,
,
那么
 ,
,

 ,
,
∴n=k+1时,猜想成立,
由①②,根据数学归纳法原理,对任意n∈N*,猜想成立;
∴当n为奇数时, ;
;
当n为偶数时, ;
;
即数列{an}的通项公式为 。
。
(Ⅲ)由(Ⅱ)得 ,
,
显然 ;
;
当n为偶数时,





 ;
;
当n为奇数时,



综上所述, 。
。
 。
。(Ⅱ)
 ,
, ,…
,… ,…
,…∴猜想:
 ,
,以下用数学归纳法证明之。
①当n=1时,
 ,猜想成立;
,猜想成立;②当n=k(k≥1,k∈N*)时,猜想成立,即
 ,
,那么

 ,
,
 ,
,∴n=k+1时,猜想成立,
由①②,根据数学归纳法原理,对任意n∈N*,猜想成立;
∴当n为奇数时,
 ;
;当n为偶数时,
 ;
;即数列{an}的通项公式为
 。
。(Ⅲ)由(Ⅱ)得
 ,
,显然
 ;
;当n为偶数时,





 ;
;当n为奇数时,



综上所述,
 。
。
练习册系列答案
相关题目
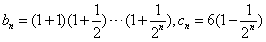 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,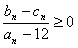 。
。 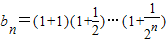 ,
,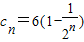 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,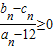 .
.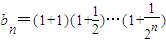 ,
,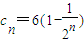 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,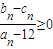 .
.