题目内容
在单调递增数列{an}中,a1=2,不等式(n+1)an≥na2n对任意n∈N*都成立,
(Ⅰ)求a2的取值范围;
(Ⅱ)判断数列{an}能否为等比数列?说明理由;
(Ⅲ)设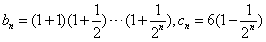 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,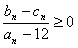 。
。
(Ⅰ)求a2的取值范围;
(Ⅱ)判断数列{an}能否为等比数列?说明理由;
(Ⅲ)设
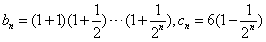 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,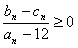 。
。 (Ⅰ)解:因为{an}是单调递增数列,所以 ,
,
令n=1, ,所以
,所以 。
。
(Ⅱ)证明:数列{an}不能为等比数列。
用反证法证明:假设数列{an}是公比为q的等比数列, ,
,
因为{an}单调递增,所以q>1,
因为n∈N*,(n+1)an≥na2n都成立,
所以n∈N*,
 , ①
, ①
因为q>1,所以 ,使得当
,使得当 时,
时, ,
,
因为 (n∈N*),
(n∈N*),
所以 ,当
,当 时,
时, ,与①矛盾,故假设不成立。
,与①矛盾,故假设不成立。
(Ⅲ)证明:观察: ,
, ,…,
,…,
猜想: ;
;
用数学归纳法证明:
(1)当n=1时, 成立;
成立;
(2)假设当n=k时, 成立;
成立;
当n=k+1时,


 ,
,
所以 ,
,
根据(1)(2)可知,对任意n∈N*,都有 ,即
,即 ,
,
由已知得 ,
,
所以 ,
,
所以当n≥2时, ,
,
因为 ,
,
所以对任意n∈N*, ,
,
对任意n∈N*,存在m∈N*,使得 ,
,
因为数列{an}单调递增,所以 ,
, ,
,
因为 ,
,
所以 。
。
 ,
,令n=1,
 ,所以
,所以 。
。(Ⅱ)证明:数列{an}不能为等比数列。
用反证法证明:假设数列{an}是公比为q的等比数列,
 ,
,因为{an}单调递增,所以q>1,
因为n∈N*,(n+1)an≥na2n都成立,
所以n∈N*,

 , ①
, ① 因为q>1,所以
 ,使得当
,使得当 时,
时, ,
,因为
 (n∈N*),
(n∈N*),所以
 ,当
,当 时,
时, ,与①矛盾,故假设不成立。
,与①矛盾,故假设不成立。(Ⅲ)证明:观察:
 ,
, ,…,
,…,猜想:
 ;
;用数学归纳法证明:
(1)当n=1时,
 成立;
成立;(2)假设当n=k时,
 成立;
成立;当n=k+1时,


 ,
,所以
 ,
,根据(1)(2)可知,对任意n∈N*,都有
 ,即
,即 ,
,由已知得
 ,
,所以
 ,
,所以当n≥2时,
 ,
,因为
 ,
,所以对任意n∈N*,
 ,
,对任意n∈N*,存在m∈N*,使得
 ,
,因为数列{an}单调递增,所以
 ,
, ,
,因为
 ,
,所以
 。
。 
练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
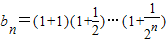 ,
,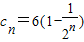 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,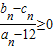 .
.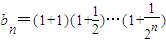 ,
,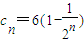 ,求证:对任意的n∈N*,
,求证:对任意的n∈N*,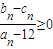 .
.