题目内容
O为△ABC平面上一定点,该平面上一动点p满足M={P|
=
+λ(
sinC+
sinB) ,λ>0},则△ABC的( )一定属于集合M.
| OP |
| OA |
| ||
|
|
| ||
|
|
| A.重心 | B.垂心 | C.外心 | D.内心 |
如图:D是BC的中点,
在△ABC中,由正弦定理得,
=

即
=
,设t=
=
,
代入
=
+λ(
sinC+
sinB)得,
=
+λt(
+
)①,
∵D是BC的中点,∴
+
=2
,代入①得,
=
+2λt
,
∴
=2λt
且λ、t都是常数,则
∥
,
∴点P得轨迹是直线AD,
△ABC的重心一定属于集合M,
故选A.
在△ABC中,由正弦定理得,
|
| ||
| sinC |
|
| ||
| sinB |

即
| sinc | ||
|
|
| sinB| | ||
|
|
| sinc | ||
|
|
| sinB| | ||
|
|
代入
| OP |
| OA |
| ||
|
|
| ||
|
|
| OP |
| OA |
| AB |
| AC |
∵D是BC的中点,∴
| AB |
| AC |
| AD |
| OP |
| OA |
| AD |
∴
| AP |
| AD |
| AP |
| AD |
∴点P得轨迹是直线AD,
△ABC的重心一定属于集合M,
故选A.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
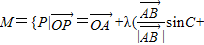
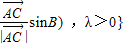 ,则△ABC的( )一定属于集合M.
,则△ABC的( )一定属于集合M.