题目内容
设函数y=f（x）与函数y=f（f（x））的定义域交集为D．若对任意的x∈D，都有f（f（x））=x，则称函数f（x）是集合M的元素．
（Ⅰ）判断函数f（x）=-x+1和g（x）=2x-1是否是集合M的元素，并说明理由；
（Ⅱ）若
，求a+b的值．
（本小题满分12分）
解：（Ⅰ）因为f（f（x））=-（-x+1）+1=x，所以f（x）∈M…
同理g（g（x））=2（2x-1）-1=4x-3，所以g（x）∉M…
（Ⅱ）因为
，所以f（f（x））=x对定义域内一切x恒成立，
即
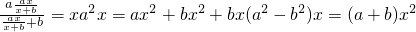恒成立
所以a+b=0…
分析：（Ⅰ）直接利用f（f（x））=x，判断函数f（x）=-x+1和g（x）=2x-1是否是集合M的元素即可．
（Ⅱ）利用新定义，通过f（f（x））=x，判断，即可求a+b的值
点评：本题考查集合的包含关系，函数的基本运算，基本知识的应用．
解：（Ⅰ）因为f（f（x））=-（-x+1）+1=x，所以f（x）∈M…
同理g（g（x））=2（2x-1）-1=4x-3，所以g（x）∉M…
（Ⅱ）因为
，所以f（f（x））=x对定义域内一切x恒成立，即
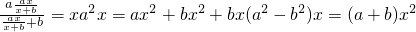恒成立所以a+b=0…
分析：（Ⅰ）直接利用f（f（x））=x，判断函数f（x）=-x+1和g（x）=2x-1是否是集合M的元素即可．
（Ⅱ）利用新定义，通过f（f（x））=x，判断
，即可求a+b的值点评：本题考查集合的包含关系，函数的基本运算，基本知识的应用．
练习册系列答案
相关题目
设函数y=f（x）与函数g（x）的图象关于x=3对称，则g（x）的表达式为（ ）
A、g(x)=f(
| ||
| B、g（x）=f（3-x） | ||
| C、g（x）=f（-3-x） | ||
| D、g（x）=f（6-x） |
