题目内容
9.已知△ABC的内角为A、B、C,其对边分别为a、b、c,B为锐角,向量$\overrightarrow{m}$=(2sin B,$\sqrt{3}$),$\overrightarrow{n}$=(2cos2$\frac{B}{2}$-1,cos 2B),且$\overrightarrow{m}$⊥$\overrightarrow{n}$;(1)求角B的大小;
(2)如果b=2,A=$\frac{5π}{12}$,求边长c.
分析 (1)由m⊥n可得2sin B•(2cos2$\frac{B}{2}$-1)+$\sqrt{3}$cos 2B=0,利用三角函数恒等变换可得2sin(2B+$\frac{π}{3}$)=0(或tan2B=-$\sqrt{3}$)结合B为锐角即可解得B的值.
(2)由三角形内角和定理可求C,由正弦定理即可求得c=$\frac{bsinC}{sinB}=\frac{2\sqrt{6}}{3}$.
解答 (本题满分为12分)
解:(1)m⊥n⇒2sin B•(2cos2$\frac{B}{2}$-1)+$\sqrt{3}$cos 2B=0…(2分)
⇒sin 2B+$\sqrt{3}$cos 2B=0…(3分)
⇒2sin(2B+$\frac{π}{3}$)=0 (或tan2B=-$\sqrt{3}$)(B为锐角)…(4分)
⇒2B=$\frac{2π}{3}$⇒B=$\frac{π}{3}$…(6分)
(2)∵B=$\frac{π}{3}$,A=$\frac{5π}{12}$,∴C=$\frac{π}{4}$…(8分)
由正弦定理$\frac{b}{sinB}=\frac{c}{sinC}$…(10分)
∴c=$\frac{bsinC}{sinB}=\frac{2\sqrt{6}}{3}$.…(12分)
点评 本题主要考查了三角形内角和定理,正弦定理,平面向量数量积的运算,三角函数恒等变换的应用,熟练掌握和灵活应用公式是解题的关键,属于中档题.

练习册系列答案
相关题目
17.下列函数中,满足“f(xy)=f(x)+f(y)”且单调递减的是( )
| A. | y=${(\frac{1}{2})}^{x}$ | B. | y=log2x | C. | $y=lo{g}_{\frac{1}{2}}x$ | D. | y=${x}^{\frac{1}{2}}$ |

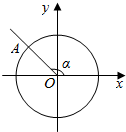 如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为$\frac{2}{3}$,则cosα=-$\frac{\sqrt{5}}{3}$.
如图所示,在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A的纵坐标为$\frac{2}{3}$,则cosα=-$\frac{\sqrt{5}}{3}$.