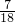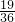题目内容
已知函数 ,集合A={1,2,3,4,5,6,7,8,9},现从A中任取两个不同的元素m,n,则f(m)•f(n)=0的概率为( )
,集合A={1,2,3,4,5,6,7,8,9},现从A中任取两个不同的元素m,n,则f(m)•f(n)=0的概率为( )A.

B.

C.

D.

【答案】分析:对于m值,求出函数的值,然后用排列组合求出满足f(m)•f(n)=0的个数,以及所有的个数,即可得到f(m)•f(n)=0的概率.
解答:解:已知函数 ,集合A={1,2,3,4,5,6,7,8,9},
,集合A={1,2,3,4,5,6,7,8,9},
现从A中任取两个不同的元素m,n,则f(m)•f(n)=0
m=3,9时 ,满足f(m)•f(n)=0的个数为m=3时8个
,满足f(m)•f(n)=0的个数为m=3时8个
m=9时8个,n=3时8个,n=9时8个,重复2个,共有30个.
从A中任取两个不同的元素m,n,则f(m)•f(n)的值有72个,
所以函数 ,集合A={1,2,3,4,5,6,7,8,9},
,集合A={1,2,3,4,5,6,7,8,9},
从A中任取两个不同的元素m,n,则f(m)•f(n)=0的概率为: =
= ,
,
故选A.
点评:本题考查概率的应用,排列组合的应用,注意满足题意,不重复不要漏,考查计算能力.
解答:解:已知函数
 ,集合A={1,2,3,4,5,6,7,8,9},
,集合A={1,2,3,4,5,6,7,8,9},现从A中任取两个不同的元素m,n,则f(m)•f(n)=0
m=3,9时
 ,满足f(m)•f(n)=0的个数为m=3时8个
,满足f(m)•f(n)=0的个数为m=3时8个m=9时8个,n=3时8个,n=9时8个,重复2个,共有30个.
从A中任取两个不同的元素m,n,则f(m)•f(n)的值有72个,
所以函数
 ,集合A={1,2,3,4,5,6,7,8,9},
,集合A={1,2,3,4,5,6,7,8,9},从A中任取两个不同的元素m,n,则f(m)•f(n)=0的概率为:
 =
= ,
,故选A.
点评:本题考查概率的应用,排列组合的应用,注意满足题意,不重复不要漏,考查计算能力.

练习册系列答案
相关题目
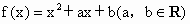 且集合A={x|x=f(x)},B={x|x=f[f(x)]}
且集合A={x|x=f(x)},B={x|x=f[f(x)]} ;
;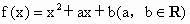 且集合A={x|x=f(x)},B={x|x=f[f(x)]}
且集合A={x|x=f(x)},B={x|x=f[f(x)]}
 ;
;
 ,集合A={1,2,3,4,5,6,7,8,9},现从A中任取两个不同的元素m,n,则f(m)•f(n)=0的概率为
,集合A={1,2,3,4,5,6,7,8,9},现从A中任取两个不同的元素m,n,则f(m)•f(n)=0的概率为