题目内容
已知向量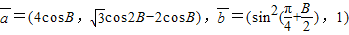 ,
,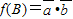
(1)若f(B)=2且0<B<π,求角B
(2)若对任意的
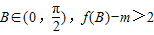 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】分析:(1)由已知中向量 ,
, ,代入向量数量积公式,利用二倍角公式及辅助角我们易得函数的解析式,进而根据f(B)=2且0<B<π,构造三角方程,即可求出角B;
,代入向量数量积公式,利用二倍角公式及辅助角我们易得函数的解析式,进而根据f(B)=2且0<B<π,构造三角方程,即可求出角B;
(2)由(1)中解析式,我们易求出当 时,函数的值域,进而根据f(B)-m>2恒成立,即函数的最小值满足f(B)-m>2,求出m的取值范围.
时,函数的值域,进而根据f(B)-m>2恒成立,即函数的最小值满足f(B)-m>2,求出m的取值范围.
解答:解:(1)∵向量 ,
, =(
=( ,1)
,1)
∴ =2cosB(1-sinB)+
=2cosB(1-sinB)+ cos2B-2cosB
cos2B-2cosB
=-sin2B+ cos2B
cos2B
=2sin(2B+ )
)
若f(B)=2,则2B+ =
= +2kπ,k∈Z
+2kπ,k∈Z
即B=- +kπ,k∈Z
+kπ,k∈Z
又∵0<B<π,
∴B=
(2)由(1)中f(B)=2sin(2B+ )
)
当 时,
时,
2B+ ∈(
∈( ,
, )
)
则f(B)∈[-2,1)
若f(B)-m>2
则m<-4
点评:本题考查的知识点是三角函数的最值,三角函数的恒等变换及化简求值,其中根据已知条件求出函数的解析式,是解答本题的关键.
 ,
, ,代入向量数量积公式,利用二倍角公式及辅助角我们易得函数的解析式,进而根据f(B)=2且0<B<π,构造三角方程,即可求出角B;
,代入向量数量积公式,利用二倍角公式及辅助角我们易得函数的解析式,进而根据f(B)=2且0<B<π,构造三角方程,即可求出角B;(2)由(1)中解析式,我们易求出当
 时,函数的值域,进而根据f(B)-m>2恒成立,即函数的最小值满足f(B)-m>2,求出m的取值范围.
时,函数的值域,进而根据f(B)-m>2恒成立,即函数的最小值满足f(B)-m>2,求出m的取值范围.解答:解:(1)∵向量
 ,
, =(
=( ,1)
,1)∴
 =2cosB(1-sinB)+
=2cosB(1-sinB)+ cos2B-2cosB
cos2B-2cosB=-sin2B+
 cos2B
cos2B=2sin(2B+
 )
)若f(B)=2,则2B+
 =
= +2kπ,k∈Z
+2kπ,k∈Z即B=-
 +kπ,k∈Z
+kπ,k∈Z又∵0<B<π,
∴B=

(2)由(1)中f(B)=2sin(2B+
 )
)当
 时,
时,2B+
 ∈(
∈( ,
, )
)则f(B)∈[-2,1)
若f(B)-m>2
则m<-4
点评:本题考查的知识点是三角函数的最值,三角函数的恒等变换及化简求值,其中根据已知条件求出函数的解析式,是解答本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 ,
,
 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.

 求f(x)解析式及单调递增区间.
求f(x)解析式及单调递增区间.
 ,求函数f(x)的最大值和最小值.
,求函数f(x)的最大值和最小值.
 。
。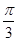 +x)的值;
+x)的值;
 。
。 +x)的值;
+x)的值;