Question

【题目】已知椭圆C： 过点A（2，3），且F（2，0）为其右焦点．
（1）求椭圆C的方程；
（2）是否存在于行于OA的直线l，使得直线l与椭圆C有公共点，且直线OA与l的距离等于 ？若存在，求出直线l的方程；若不存在，请说明理由．

Answer 1

【答案】
（1）解：∵椭圆C： 过点A（2，3），且F（2，0）为其右焦点，

∴椭圆C的左焦点为F′（﹣2，0），则|AF|=3，|AF′|= =5，

∴ ，即 ，∴b2=16﹣4=12，

∴椭圆C的方程为 =1．

（2）解：设存在符合题意的直线l，其方程为y= ，

由 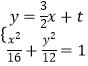，整理，得3x2+3tx+t2﹣12=0，

∵直线l与椭圆C有公共点，

∴△=（3t）2﹣12（t2﹣12）=﹣3t2+144≥0，

解得﹣4 ，

∵直线OA与l的距离等于 ，∴ = ，故t=±5．

∵±5∈[﹣4 ，4 ]，

∴直线l的方程为y= 或y=

【解析】（1）利用椭圆焦点和椭圆定义，求出a，b，由此能求出椭圆C的方程．（2）设存在符合题意的直线l，其方程为y= ，与椭圆联立，得3x2+3tx+t2﹣12=0，由此利用根的判别式、点到直线的距离公式，能求出结果方程．