题目内容
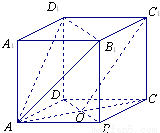
在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.(1)求证:C1O∥平面AB1D1;
(2)求直线AC与平面AB1D1所成角的大小.
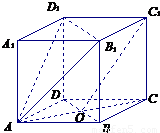
【答案】分析:(1)连接A1C1,交B1D1于O1,证明四边形AOC1O1为平行四边形,从而由线线平行即AO1∥OC1,推证出线面平行即C1O∥平面AB1D1
(2)先证明平面AB1D1⊥平面A1C,由面面垂直的性质定理可知,过C作平面AB1D1的垂线,垂足一定在交线上,从而∠O1AO就是直线AC与平面AB1D1所成的角,最后在三角形
O1OA中计算此角即可
解答:解:(1)连接A1C1,交B1D1于O1
在矩形ACA1C1中,易得O1C1∥A0,且O1C1=A0
∴四边形AOC1O1为平行四边形
∴AO1∥OC1,∵AO1?平面AB1D1;
∴C1O∥平面AB1D1;
(2)∵B1D1⊥A1C1,B1D1⊥A1A,
∴B1D1⊥平面A1C,
∴平面AB1D1⊥平面A1C,交线为AO1;
∴点C在平面AB1D1⊥上的射影一定在交线AO1上
∴∠O1AO就是直线AC与平面AB1D1所成的角
在Rt△O1OA中,AO= ,O1O=|AB|
,O1O=|AB|
∴tan∠O1AO=
∴直线AC与平面AB1D1所成的角为arctan
点评:本题考察了线面平行的证明方法和线面角的作法和求法,解题时要熟记线面平行的判定定理,熟记面面垂直的性质定理,能将空间问题转化为平面问题解决
(2)先证明平面AB1D1⊥平面A1C,由面面垂直的性质定理可知,过C作平面AB1D1的垂线,垂足一定在交线上,从而∠O1AO就是直线AC与平面AB1D1所成的角,最后在三角形
O1OA中计算此角即可
解答:解:(1)连接A1C1,交B1D1于O1
在矩形ACA1C1中,易得O1C1∥A0,且O1C1=A0
∴四边形AOC1O1为平行四边形
∴AO1∥OC1,∵AO1?平面AB1D1;
∴C1O∥平面AB1D1;
(2)∵B1D1⊥A1C1,B1D1⊥A1A,
∴B1D1⊥平面A1C,
∴平面AB1D1⊥平面A1C,交线为AO1;
∴点C在平面AB1D1⊥上的射影一定在交线AO1上
∴∠O1AO就是直线AC与平面AB1D1所成的角
在Rt△O1OA中,AO=
 ,O1O=|AB|
,O1O=|AB|∴tan∠O1AO=

∴直线AC与平面AB1D1所成的角为arctan

点评:本题考察了线面平行的证明方法和线面角的作法和求法,解题时要熟记线面平行的判定定理,熟记面面垂直的性质定理,能将空间问题转化为平面问题解决

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
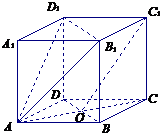 在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.
在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.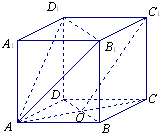 在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.
在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1. 在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.
在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.