题目内容
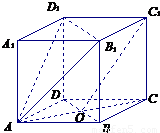
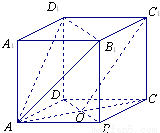
 在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.
在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.(1)求证:C1O∥平面AB1D1;
(2)求证:平面AB1D1⊥平面ACC1A1;
(3)求直线AC与平面AB1D1所成角的正弦值.
分析:(1)连接A1C1交B1D1于O1,连接AO1;可以推得四边形AOC1O1为平行四边形;进而得到C1O∥AO1,再结合线面平行的判定即可证明结论.
(2)先根据直平行六面体AC1中,A1A⊥平面A1B1C1D1,得到A1A⊥B1D1;再结合四边形A1B1C1D1为菱形,得到B1D1⊥A1C1;即可得到平面AB1D1⊥平面ACC1A1;
(3)过C作CH⊥AO1交AO1于H,可得CH⊥平面AB1D1;进而得∠CAH是AC与平面AB1D1所成的角;然后通过求三角形的边长即可求出结论.
(2)先根据直平行六面体AC1中,A1A⊥平面A1B1C1D1,得到A1A⊥B1D1;再结合四边形A1B1C1D1为菱形,得到B1D1⊥A1C1;即可得到平面AB1D1⊥平面ACC1A1;
(3)过C作CH⊥AO1交AO1于H,可得CH⊥平面AB1D1;进而得∠CAH是AC与平面AB1D1所成的角;然后通过求三角形的边长即可求出结论.
解答: 证明:(1)连接A1C1交B1D1于O1,连接AO1.
证明:(1)连接A1C1交B1D1于O1,连接AO1.
在平行四边形AA1C1C中,C1O1∥AO,C1O1=AO,
∴四边形AOC1O1为平行四边形.
∴C1O∥AO1.(3分)
∵C1O?平面AB1D1,AO1?平面AB1D1,(4分)
∴C1O∥平面AB1D1.(5分)
(2)在直平行六面体AC1中,A1A⊥平面A1B1C1D1,
∴A1A⊥B1D1.
∵四边形A1B1C1D1为菱形,
∴B1D1⊥A1C1.(7分)
∵A1C1∩AA1=A1,A1C1?平面ACC1A1,AA1?平面ACC1A1,(9分)
∴B1D1⊥平面ACC1A1.
∵B1D1?平面AB1D1,
∴平面AB1D1⊥平面ACC1A1.(10分)
(3)过C作CH⊥AO1交AO1于H.
∵平面AB1D1⊥平面ACC1A1,平面AB1D1∩平面ACC1A1=AO1,
∴CH⊥平面AB1D1.
∴AH为AC在平面AB1D1上的射影.
∴∠CAH是AC与平面AB1D1所成的角.(11分)
设AB=2,在菱形ABCD中,∠DAB=60°,
∴AC=2
.(12分)
在Rt△AA1O1中,AO1=
.
∵AO1•CH=AC•OO1,
∴CH=
.∴sinCAH=
=
.(14分)
 证明:(1)连接A1C1交B1D1于O1,连接AO1.
证明:(1)连接A1C1交B1D1于O1,连接AO1.在平行四边形AA1C1C中,C1O1∥AO,C1O1=AO,
∴四边形AOC1O1为平行四边形.
∴C1O∥AO1.(3分)
∵C1O?平面AB1D1,AO1?平面AB1D1,(4分)
∴C1O∥平面AB1D1.(5分)
(2)在直平行六面体AC1中,A1A⊥平面A1B1C1D1,
∴A1A⊥B1D1.
∵四边形A1B1C1D1为菱形,
∴B1D1⊥A1C1.(7分)
∵A1C1∩AA1=A1,A1C1?平面ACC1A1,AA1?平面ACC1A1,(9分)
∴B1D1⊥平面ACC1A1.
∵B1D1?平面AB1D1,
∴平面AB1D1⊥平面ACC1A1.(10分)
(3)过C作CH⊥AO1交AO1于H.

∵平面AB1D1⊥平面ACC1A1,平面AB1D1∩平面ACC1A1=AO1,
∴CH⊥平面AB1D1.
∴AH为AC在平面AB1D1上的射影.
∴∠CAH是AC与平面AB1D1所成的角.(11分)
设AB=2,在菱形ABCD中,∠DAB=60°,
∴AC=2
| 3 |
在Rt△AA1O1中,AO1=
| 7 |
∵AO1•CH=AC•OO1,
∴CH=
4
| ||
| 7 |
.∴sinCAH=
| CH |
| AC |
2
| ||
| 7 |
点评:本题主要考察线面平行以及面面垂直的证明,线面角的求法.一般在证明面面垂直时,先证明线线垂直,得到线面垂直,进而得到面面垂直.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
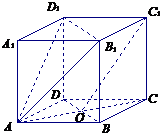 在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.
在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.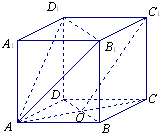 在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.
在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.