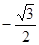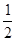题目内容
已知函数 ,在下列给出结论中:
,在下列给出结论中:
① 是
是 的一个周期;
的一个周期;
② 的图象关于直线
的图象关于直线
 对称;
对称;
③ 在
在 上单调递减.
上单调递减.
其中,正确结论的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
C
解析试题分析:因为, ,
, ,所以,①不正确;
,所以,①不正确;
又 ,
,
由满足 ,其图象的对称轴为
,其图象的对称轴为 ,所以,②正确;
,所以,②正确;
因为, ,
, 在
在 上均为增函数,
上均为增函数,
所以, 在
在 上为减函数,③正确.
上为减函数,③正确.
综上知,正确结论的个数为2,选C.
考点:三角函数的图象和性质

练习册系列答案
相关题目
已知函数 ,若有四个不同的正数
,若有四个不同的正数 满足
满足 (
( 为常数),且
为常数),且 ,
, ,则
,则 的值为( )
的值为( )
| A.10 | B.14 | C.12 | D.12或20 |
已知 ,则
,则 ( )
( )
A. | B. | C. | D. |
函数 (其中
(其中 )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图像,则只要将
的图像,则只要将 的图像( )
的图像( )
A.向右平移 个单位长度 个单位长度 | B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 | D.向左平移 个单位长度 个单位长度 |
若实数 满足
满足 ,则
,则 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
已知函数 ,若
,若 ,且
,且 ,则
,则 的最小值为( )
的最小值为( )
A.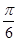 | B. | C. | D. |
已知 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
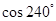 的值是( )
的值是( )
A. | B.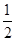 | C.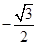 | D. |
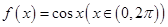 有两个不同的零点
有两个不同的零点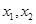 ,方程
,方程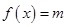 有两个不同的实根
有两个不同的实根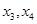 .若这四个数按从小到大排列构成等差数列,则实数
.若这四个数按从小到大排列构成等差数列,则实数 的值为( )
的值为( )