题目内容
集合A={x|x2-ax+a2-19=0},B={x|log2(x2-5x+8)=1},C={x|x2+2x-8=0},求当a取什么实数时,A∩B 
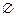 和A∩C=
和A∩C=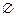 同时成立.
同时成立.


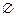 和A∩C=
和A∩C=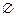 同时成立.
同时成立.
log2(x2-5x+8)=1,由此得x2-5x+8=2,∴B={2,3} 由x2+2x-8=0,∴C={2,-4},又A∩C=
由x2+2x-8=0,∴C={2,-4},又A∩C=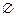 ,∴2和-4都不是关于x的方程x2-ax+a2-19=0的解,而A∩B
,∴2和-4都不是关于x的方程x2-ax+a2-19=0的解,而A∩B 
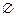 ,即A∩B≠
,即A∩B≠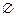 ,
,
∴3是关于x的方程x2-ax+a2-19=0的解,∴可得a=5或a=-2.
当a=5时,得A={2,3},∴A∩C={2},这与A∩C=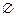 不符合,所以a=5(舍去);当a=-2时,可以求得A={3,-5},符合A∩C=
不符合,所以a=5(舍去);当a=-2时,可以求得A={3,-5},符合A∩C=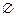 ,A∩B
,A∩B 
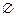 ,∴a=-2.
,∴a=-2.
 由x2+2x-8=0,∴C={2,-4},又A∩C=
由x2+2x-8=0,∴C={2,-4},又A∩C=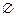 ,∴2和-4都不是关于x的方程x2-ax+a2-19=0的解,而A∩B
,∴2和-4都不是关于x的方程x2-ax+a2-19=0的解,而A∩B 
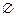 ,即A∩B≠
,即A∩B≠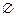 ,
,∴3是关于x的方程x2-ax+a2-19=0的解,∴可得a=5或a=-2.
当a=5时,得A={2,3},∴A∩C={2},这与A∩C=
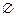 不符合,所以a=5(舍去);当a=-2时,可以求得A={3,-5},符合A∩C=
不符合,所以a=5(舍去);当a=-2时,可以求得A={3,-5},符合A∩C=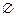 ,A∩B
,A∩B 
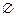 ,∴a=-2.
,∴a=-2.
练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 也可表示为
也可表示为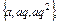 其中a,d,q
其中a,d,q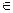 R,求常数q.
R,求常数q.
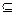 B;
B;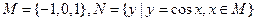 ,则集合N的真子集个数为( )
,则集合N的真子集个数为( )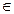 Z},B={1,2,3,4},全集U=AUB,则集合C
Z},B={1,2,3,4},全集U=AUB,则集合C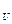 (A
(A 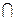 B)的子集个数为
B)的子集个数为