题目内容
如图，已知四边形ABCD是正方形，PD⊥平面ABCD，若AB=a,PD=a,求：(1)P到正方形各顶点的距离；
(2)P到正方形各边的距离；
(3)P到两条对角线的距离.
解析：(1)P到各顶点的距离分别为PA、PB、PC、PD的长.?
∵PD⊥平面ABCD，AB⊥AD，?
∴PA⊥AB.?
∴△PAB为直角三角形.?
同理，△PAD、△PCD、△PBD也是直角三角形.?
∵PD=a,AB=a,ABCD为正方形，?
∴PA=2a,PB=3a,PC=2a,PD=a.?
(2)由图形易知P到AD、CD的距离都是PD=a.P到BC的距离为PC，P到AB的距离为PA，即为
.?
(3)∵AC⊥BD,?
∴DO⊥AC.?
又∵PD⊥平面ABCD，AO
平面ABCD，?
∴PD⊥AC.?
∴PO⊥AC.?
故PO的长就是P到对角线AC的距离?
PO=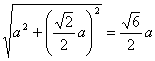
.?
而P到对角线BD的距离为PD的长，PD=a.?
故P到BD的距离为a，到AC的距离为
.
练习册系列答案
相关题目
如图，已知四边形ABCD为直角梯形，∠ABC=90°，AD∥BC，AD=2，AB=BC=1，沿AC将△ABC折起，使点B到点P的位置，且平面PAC⊥平面ACD．
（几何证明选讲选做题）如图，已知四边形ABCD内接于⊙O，且AB为⊙O的直径，直线MN切
如图：已知四边形ABCD是正方形，PD⊥平面ABCD，PD=AD，点E，F分别是线段PB，AD的中点
如图，已知四边形ABCD为直角梯形，∠ABC=90°，AD∥BC，AD=2，AB=BC=1，沿AC将△ABC折起，使点B到点P的位置，且平面PAC⊥平面ACD．
如图，已知四边形ABCD是菱形，PA⊥平面ABCD，PA=AB=BD=2，AC与BD交于E点，F是PD的中点．