题目内容
(本小题满分13分)已知点 在椭圆
在椭圆 上,椭圆
上,椭圆 的左焦点为(-1,0)
的左焦点为(-1,0)

(1)求椭圆 的方程;
的方程;
(2)直线 过点
过点 交椭圆C于M、N两点,AB是椭圆
交椭圆C于M、N两点,AB是椭圆 经过原点
经过原点 的弦,且MN//AB,问是否存在正数
的弦,且MN//AB,问是否存在正数 ,使
,使 为定值?若存在,求出
为定值?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)  ;(2)m=1
;(2)m=1
【解析】
试题分析:(1)椭圆C的左焦点为(1,0),∴c=1,椭圆C的右焦点为(-1,0)
可得 ,解得a=2, 2分
,解得a=2, 2分
∴ ∴椭圆C的标准方程为
∴椭圆C的标准方程为 4分
4分
(2)设直线 ,且
,且 ,由
,由
得 6分
6分
8分
由 得
得
设
得 得
得 10分
10分
而
∴当 时
时
 为定值,当k不存在时,定值也为4,∴m=1 13分
为定值,当k不存在时,定值也为4,∴m=1 13分
考点:本题考查椭圆的标准方程,直线与椭圆的位置关系

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,设函数
,设函数 在区间
在区间 上的最大值为
上的最大值为 .
. ,试求出
,试求出 对任意的
对任意的 恒成立,试求
恒成立,试求 的最大值.
的最大值. ,则( )
,则( ) 是不等式组
是不等式组 表示的平面区域内的任意一点,向量
表示的平面区域内的任意一点,向量 ,
, ,若
,若 (
( ,
, 为实数),则
为实数),则 的最大值为( )
的最大值为( )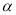 与平面
与平面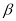 相交于直线
相交于直线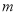 ,直线
,直线 在平面
在平面 在平面
在平面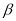 内,且
内,且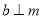 ,则“
,则“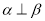 ”是“
”是“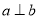 ”的( )
”的( ) :
: 的焦点为
的焦点为 ,准线为
,准线为 ,
, 是
是 上一点,
上一点, 是直线
是直线 与
与 ,则
,则 = .
= . ,则向量
,则向量 与
与 的夹角为( )
的夹角为( ) B.
B. C.
C. D.
D.
 个等式为 .
个等式为 .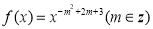 为偶函数,且在区间
为偶函数,且在区间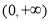 上是单调增函数
上是单调增函数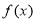 的解析式;
的解析式;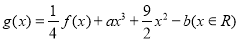 ,其中
,其中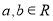 .若函数
.若函数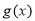 仅在
仅在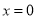 处有极值,求
处有极值,求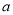 的取值范围.
的取值范围.