题目内容
已知⊙C1：x2+y2-6x-2y+6=0，⊙C2：x2+y2-2x-4y+4=0，试在两圆公共弦所在直线上求一点P，使P到两圆的切线长为3．
考点：圆的切线方程
专题：直线与圆
分析：由题意求出圆心坐标和半径，将两圆方程相减得公共弦所在直线方程，设出P的坐标，根据切线长公式列出方程，求出x的值，代入直线方程求出y，即求出点P的坐标．
解答：
解：由题意得，⊙C1：x2+y2-6x-2y+6=0，⊙C2：x2+y2-2x-4y+4=0，
所以C1（3，1），半径r1=2，C2（1，2），r2=1，
将两圆方程相减得，公共弦所在直线方程为4x-2y-2=0，即2x-y-1=0，
所以设P（x，2x-1），
因为P到两圆的切线长为3，
所以由勾股定理得，（x-3）2+（2x-1-1）2-4=（x-1）2+（2x-1-2）2-1=9
解得，x=0 或 x=
，代入2x-y-1=0，解得y=-1或
，
因此，所求P的坐标为（0，-1）或（
，
）．
所以C1（3，1），半径r1=2，C2（1，2），r2=1，
将两圆方程相减得，公共弦所在直线方程为4x-2y-2=0，即2x-y-1=0，
所以设P（x，2x-1），
因为P到两圆的切线长为3，
所以由勾股定理得，（x-3）2+（2x-1-1）2-4=（x-1）2+（2x-1-2）2-1=9
解得，x=0 或 x=
| 14 |
| 5 |
| 23 |
| 5 |
因此，所求P的坐标为（0，-1）或（
| 14 |
| 5 |
| 23 |
| 5 |
点评：本题考查两圆相交时公共弦所在直线方程，以及切线长公式，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知sin10°=k，则sin110°=（ ）
| A、1-k2 |
| B、2k2-1 |
| C、1-2k2 |
| D、1+2k2 |
命题“?x＞0，x-lnx＞0”的否定是（ ）
| A、?x＞0，x-lnx≤0 |
| B、?x＞0，x-lnx＜0 |
| C、?x＞0，x-lnx＜0 |
| D、?x＞0，x-lnx≤0 |
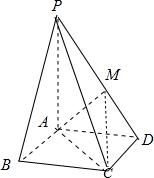如图，四棱锥P-ABCD的底面ABCD是矩形，侧棱PA⊥底面ABCD，PA=2