题目内容
函数y=ln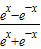 的图象大致为( )
的图象大致为( )A.
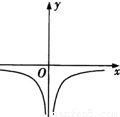
B.
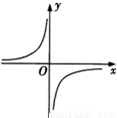
C.
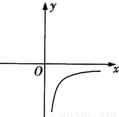
D.
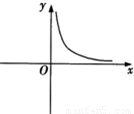
【答案】分析:化简函数的解析式为ln(1-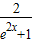 ),求出它的定义域为(0,+∞),y<0,且y是(0,+∞)上的增函数,结合所给的选项,得出结论.
),求出它的定义域为(0,+∞),y<0,且y是(0,+∞)上的增函数,结合所给的选项,得出结论.
解答:解:∵函数y=ln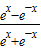 =ln
=ln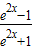 =ln(1-
=ln(1-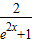 ),由 1-
),由 1-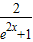 >0 可得x>0,
>0 可得x>0,
故函数的定义域为(0,+∞).
再由 0<1-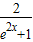 <1,可得 y<0,且y是(0,+∞)上的增函数,
<1,可得 y<0,且y是(0,+∞)上的增函数,
故选C.
点评:本题主要考查函数的图象特征,函数的定义域和单调性的应用,属于基础题.
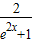 ),求出它的定义域为(0,+∞),y<0,且y是(0,+∞)上的增函数,结合所给的选项,得出结论.
),求出它的定义域为(0,+∞),y<0,且y是(0,+∞)上的增函数,结合所给的选项,得出结论.解答:解:∵函数y=ln
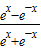 =ln
=ln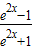 =ln(1-
=ln(1-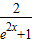 ),由 1-
),由 1-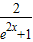 >0 可得x>0,
>0 可得x>0,故函数的定义域为(0,+∞).
再由 0<1-
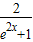 <1,可得 y<0,且y是(0,+∞)上的增函数,
<1,可得 y<0,且y是(0,+∞)上的增函数,故选C.
点评:本题主要考查函数的图象特征,函数的定义域和单调性的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ax2+bx(a>0),且f′(1)=0
ax2+bx(a>0),且f′(1)=0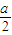 )-1
)-1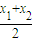 时,则称AB存在“中值相依切线”.请问在函数f(x)的图象上是否存在两点A(x1,y1),B(x2,y2),使得AB存在“中值相依切线”?若存在,求出一组A、B的坐标;若不存在,说明理由.
时,则称AB存在“中值相依切线”.请问在函数f(x)的图象上是否存在两点A(x1,y1),B(x2,y2),使得AB存在“中值相依切线”?若存在,求出一组A、B的坐标;若不存在,说明理由.