题目内容
设定义在R上的奇函数y=f(x),满足对任意t∈R都有f(t)=f(1-t),且x 时,f(x)=-x2,则f(3)+f(-
时,f(x)=-x2,则f(3)+f(-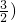 的值等于
的值等于
- A.-

- B.-

- C.-

- D.-

C
分析:利用奇函数的性质和对任意t∈R都有f(t)=f(1-t),即可分别得到f(3)=f(0), .再利用x
.再利用x 时,f(x)=-x2,即可得出答案.
时,f(x)=-x2,即可得出答案.
解答:∵定义在R上的奇函数y=f(x),满足对任意t∈R都有f(t)=f(1-t),
∴f(3)=f(1-3)=f(-2)=-f(2)=-f(1-2)=f(1)=f(1-1)=f(0),
 =
= .
.
∵x 时,f(x)=-x2,∴f(0)=0,
时,f(x)=-x2,∴f(0)=0, ,
,
∴f(3)+f(-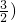 =0
=0 .
.
故选C.
点评:熟练掌握函数的奇偶性和对称性是解题的关键.
分析:利用奇函数的性质和对任意t∈R都有f(t)=f(1-t),即可分别得到f(3)=f(0),
 .再利用x
.再利用x 时,f(x)=-x2,即可得出答案.
时,f(x)=-x2,即可得出答案.解答:∵定义在R上的奇函数y=f(x),满足对任意t∈R都有f(t)=f(1-t),
∴f(3)=f(1-3)=f(-2)=-f(2)=-f(1-2)=f(1)=f(1-1)=f(0),
 =
= .
.∵x
 时,f(x)=-x2,∴f(0)=0,
时,f(x)=-x2,∴f(0)=0, ,
,∴f(3)+f(-
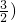 =0
=0 .
.故选C.
点评:熟练掌握函数的奇偶性和对称性是解题的关键.

练习册系列答案
相关题目