题目内容
定义在 上的函数
上的函数
 的单调增区间为
的单调增区间为 ,若方程
,若方程 恰有4个不同的实根,则实数
恰有4个不同的实根,则实数 的值为( )
的值为( )
A. | B. | C.1 | D.-1 |
B
解析试题分析:∵函数
 的单调增区间为
的单调增区间为 ,∴-1和1是
,∴-1和1是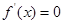 的根,
的根,
∴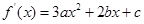 ,∴
,∴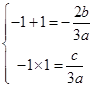 ,∴
,∴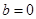 ,
,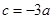 ,∴
,∴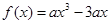 ,
,
∴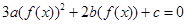 ,∴
,∴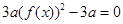 ,∴
,∴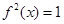 ,∴
,∴ ,
,
∴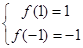 ,∴
,∴ .
.
考点:1.函数的单调性;2.韦达定理;3.函数的最值.

练习册系列答案
相关题目
如图,点 从点
从点 出发,分别按逆时针方向沿周长均为
出发,分别按逆时针方向沿周长均为 的正三角形、正方形运动一周,
的正三角形、正方形运动一周, 两点连线的距离
两点连线的距离 与点
与点 走过的路程
走过的路程 的函数关系分别记为
的函数关系分别记为 ,定义函数
,定义函数 对于函数
对于函数 ,下列结论正确的个数是( )
,下列结论正确的个数是( )
① ;
;
②函数 的图像关于直线
的图像关于直线 对称;
对称;
③函数 值域为
值域为 ;
;
④函数 在区间
在区间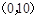 上单调递增.
上单调递增.
| A.1 | B.2 | C.3 | D.4 |
函数 若关于
若关于 的方程
的方程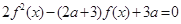 有五个不同的实数解,则
有五个不同的实数解,则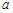 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
已知函数 ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.若 ,则 ,则 恒成立 恒成立 |
B.若 恒成立,则 恒成立,则 |
C.若 ,则关于 ,则关于 的方程 的方程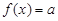 有解 有解 |
D.若关于 的方程 的方程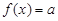 有解,则 有解,则 |
函数 图象交点的横坐标所在区间是( )
图象交点的横坐标所在区间是( )
| A.(1,2) | B.(2,3) | C.(3,4) | D.(1,5) |
已知 满足对任意
满足对任意 成立,那么
成立,那么 的取值范围是( )
的取值范围是( )
A. | B. | C.(1,2) | D. |
 的图像可能是( )
的图像可能是( )
 的图象是 ( )
的图象是 ( )
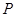 在边长为1的正方形的边上运动,
在边长为1的正方形的边上运动, 是
是 的中点,则当
的中点,则当 运动时,点
运动时,点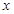 与
与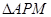 的面积
的面积 的函数
的函数 的图像的形状大致是下图中的( ).
的图像的形状大致是下图中的( ).
