题目内容
已知A，B两地位于北纬45°的纬线上，且两地的经度之差为90°，设地球的半径为Rkm，则时速为20km的轮船从A地到B地，最少需要的小时数是（ ）A．
B．
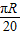
C．
D．
【答案】分析：设北纬45°纬线的小圆圆心为Q，算出△AOB是等边三角形，得∠AOB=60°，从而得到甲、乙两地的球面距离为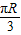
，结合轮船的时速为20km即可算出最少需要的小时数．
解答：解：如图，设北纬45°纬线的小圆圆心为Q
由题意知：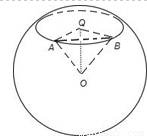
∠QAO=∠QBO=45°，∠AQB=90°，
∴△QAB≌△QAO
可得AB=AO=BO=Rkm
∴△AOB是等边三角形，得∠AOB=60°，
得到甲、乙两地的最短距离即球面距离为：s=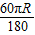
=
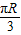
因此，时速为20km的轮船从A地到B地，最少需要t=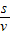
=
=
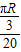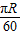
故选：D
点评：本题给出实际应用问题，求轮船从A地到B地最少需要的小时数．着重考查了球面距离的计算及其实际应用等知识，属于中档题．
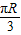，结合轮船的时速为20km即可算出最少需要的小时数．解答：解：如图，设北纬45°纬线的小圆圆心为Q
由题意知：
∠QAO=∠QBO=45°，∠AQB=90°，∴△QAB≌△QAO
可得AB=AO=BO=Rkm
∴△AOB是等边三角形，得∠AOB=60°，
得到甲、乙两地的最短距离即球面距离为：s=
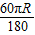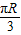
=因此，时速为20km的轮船从A地到B地，最少需要t=
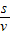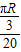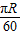
==故选：D
点评：本题给出实际应用问题，求轮船从A地到B地最少需要的小时数．着重考查了球面距离的计算及其实际应用等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
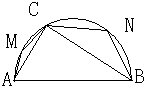已知 A、B两地相距2R，以AB为直径作一个半圆，在半圆上取一点C，连接AC、BC，在三角形ABC内种草坪（如图），M、N分别为弧AC、弧BC的中点，在三角形AMC、三角形BNC上种花，其余是空地．设花坛的面积为S1，草坪的面积为S2，取∠ABC=θ．设A、B两地位于北纬α的纬线上，且两地的经度差为90°，若地球的半径为R千米，且时速为20千米的轮船从A地到B地最少需要
小时，则α为（ ）
| πR |
| 60 |
A、
| ||
B、
| ||
C、
| ||
D、
|