Question

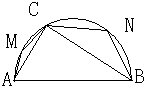已知 A、B两地相距2R，以AB为直径作一个半圆，在半圆上取一点C，连接AC、BC，在三角形ABC内种草坪（如图），M、N分别为弧AC、弧BC的中点，在三角形AMC、三角形BNC上种花，其余是空地．设花坛的面积为S₁，草坪的面积为S₂，取∠ABC=θ．
（1）用θ及R表示S₁和S₂；
（2）求

S1

S2

的最小值．

Answer 1

分析：（1）先利用θ及R表示出AC、BC的长，进而求出S₂；再设AB的中点为O，连MO、NO，则MO⊥AC，NO⊥BC，即可求出三角形AMC、三角形BNC的面积，进而求得S₁；
（2）先利用（1）的结论求出

S1

S2

关于θ的表达式；再结合三角函数以及函数单调性的知识即可求出

S1

S2

的最小值．

解答：解：（1）因为∠ABC=θ，则AC=2Rsinθ，BC=2Rcosθ，
则S2=

1

2

AC•BC=2R2sinθcosθ=R2sin2θ．（3分）
设AB的中点为O，连MO、NO，则MO⊥AC，NO⊥BC．
设MO交AC与点E．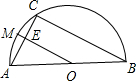
则ME=MO-OE=R-

BC

2

=R-Rcosθ=R（1-cosθ）．
所以：S_△AMC=

1

2

|AC|•|ME|=R²sinθ（1-cosθ）；（5分）
同理可得三角形BNC的面积为R²cosθ（1-sinθ），（7分）
∴S₁=R²sinθ（1-cosθ）+R²cosθ（1-sinθ）=R²（sinθ+cosθ-2sinθcosθ）．（8分）
（2）∵

S1

S2

=

R2(sinθ+cosθ-2sinθcosθ)

2R2sinθcosθ

=

sinθ+cosθ

2sinθcosθ

-1，（10分）
令sinθ+cosθ=t∈(1，

2

]，则2sinθcosθ=t²-1．
∴

S1

S2

=

t

t2-1

-1=

1

t- 1 t

-1．（12分）
∴

S1

S2

的最小值为

2

-1．（14分）

点评：本题主要考查三角函数知识与实际生活相结合问题．解决本题的关键在与利用三角形的有关知识求出S₁和S₂．