Question

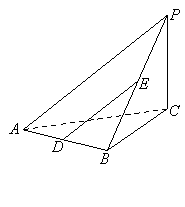
【题目】如图11所示，三棱台中， ， ， 分别为的中点.

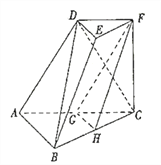
（1）求证： 平面；

（2）若， ,求证：平面平面.

Answer 1

【答案】详见解析

【解析】试题分析：（1）如图所示，连接DG，CD，设CD∩GF=M，连接MH．由已知可得四边形CFDG是平行四边形，DM=MC．利用三角形的中位线定理可得：MH∥BD，可得BD∥平面FGH；（2）连接HE，利用三角形中位线定理可得GH∥AB，于是GH⊥BC．可证明EFCH是平行四边形，可得HE⊥BC．因此BC⊥平面EGH，即可证明平面BCD⊥平面EGH．

试题解析：

（1）连接,设，连接.在三棱台中， ， 为 的中点，可得， ，所以四边形为平行四边形，则为的中点，又为的中点，所以.又平面， 平面，所以平面.

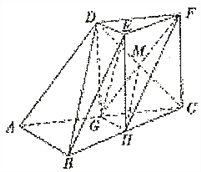
（2）连接.

因为, 分别为， 的中点，

所以.

由，得.

又为的中点，

所以， ，

因此四边形是平行四边形.

所以.

又，所以.

又， 平面，

，

所以平面.

又平面，所以平面平面.