题目内容
△ABC的三个顶点的坐标是A(5,1),B(7,－3),C(2,－8),求它的外接圆的方程.
活动:教师引导学生从圆的标准方程(x－a)2+(y－b)2=r2入手,要确定圆的标准方程,可用待定系数法确定a、b、r三个参数.另外可利用直线AB与AC垂直平分线的交点确定圆心,从而得半径,圆的方程可求,师生总结、归纳,提炼方法.
解法一:设所求圆的标准方程为(x－a)2+(y－b)2=r2,因为A(5,1),B(7,－3),C(2,－8)都在圆上,它们的坐标都满足方程(x－a)2+(y－b)2=r2,于是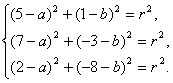
解此方程组得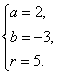
所以△ABC的外接圆的方程为(x－2)2+(y+3)2=25.
解法二:线段AB的中点坐标为(6,-1),斜率为-2,所以线段AB的垂直平分线的方程为y+1=
(x-6),即x-2y-8=0.①
同理,线段AC的中点坐标为(
,
),斜率为3,所以线段AC的垂直平分线的方程为y+
=
(x
),即x+3y+7=0.②
解由①②组成的方程组得x=2,y=-3,所以圆心坐标为(2,-3),半径r=
=5.所以△ABC的外接圆的方程为(x－2)2+(y+3)2=25.
点评:△ABC外接圆的圆心是△ABC的外心,它是△ABC三边的垂直平分线的交点,它到三顶点的距离相等,就是圆的半径,利用这些几何知识,可丰富解题思路.
练习册系列答案
相关题目