题目内容
13．借助计算器用二分法求函数f（x）=3x-$\sqrt{2-x}$可在区间（0，1）内的零点（精度为0.1）．分析 直接由计算器求出区间（0，1）的端点出的函数值及其区间中点处的函数值，直至区间端点差的绝对值满足精确度为止，则答案可求．
解答 解：f（x）=3x-$\sqrt{2-x}$，因为，f（0）=30-$\sqrt{2}$＜0，f（1）=3-1＞0，所以函数在（0，1）内存在零点，即方程3x-$\sqrt{2-x}$=0在（0，1）内有实数根．
取（0，1）的中点0.5，经计算f（0.5）＞0，又f（0）＜0，所以方程3x-$\sqrt{2-x}$=0在（0.0.5）内有实数根．
如此继续下去，得到方程的一个实数根所在的区间，如下表：
| （a，b） | （a，b） 的中点 | f（a） | f（b） | f（$\frac{a+b}{2}$ ） |
| （0，1） | 0.5 | f（0）＜0 | f（1）＞0 | f（0.5）＞0 |
| （0，0.5） | 0.25 | f（0）＜0 | f（0.5）＞0 | f（0.25）＜0 |
| （0.25，0.5） | 0.375 | f（0.25）＜0 | f（0.5）＞0 | f（0.375）＞0 |
| （0.25，0.375） | 0.3125 | f（0.25）＜0 | f（0.375）＞0 | f（0.3125）＞0 |
点评 本题主要考查用二分法求方程的近似解的方法和步骤，函数的零点与方程的根的关系，属于基础题
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
18．分层抽样适合的总体是（ ）
| A． | 总体容量较多 | B． | 样本容量较多 | ||
| C． | 总体中个体有差异 | D． | 任何总体 |
5．
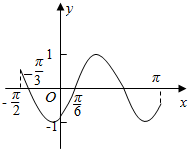若函数y=sin（ωx-φ）（ω＞0，|φ|＜π）在区间$[{-\frac{π}{2}，π}]$的简图如图所示，则ω，φ的值分别是（ ）
若函数y=sin（ωx-φ）（ω＞0，|φ|＜π）在区间$[{-\frac{π}{2}，π}]$的简图如图所示，则ω，φ的值分别是（ ）| A． | $ω=2，φ=\frac{π}{3}$ | B． | $ω=2，φ=-\frac{2π}{3}$ | C． | $ω=\frac{1}{2}，φ=\frac{π}{3}$ | D． | $ω=\frac{1}{2}，φ=-\frac{2π}{3}$ |
2．下列两个函数表示相等函数的是（ ）
| A． | f（x）=lgx2，g（x）=2lgx | B． | f（x）=1，g（x）=x0 | ||
| C． | $f（x）=\sqrt{x^2}，g（x）={（\sqrt{x}）^2}$ | D． | $f（x）=x，g（x）={log_a}{a^x}（a＞0且a≠1）$ |